(本小题满分12分)为了研究某种细菌在特定环境下,随时间变化繁殖情况,得如下实验数据:
| 天数t(天) |
3 |
4 |
5 |
6 |
7 |
| 繁殖个数y(千个) |
2.5 |
3 |
4 |
4.5 |
6 |
(Ⅰ)求y关于t的线性回归方程;
(Ⅱ)利用(Ⅰ)中的回归方程,预测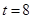 时,细菌繁殖个数.
时,细菌繁殖个数.
附:回归直线的斜率和截距的最小二乘法估计公式分别为:
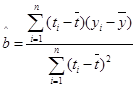 ,
,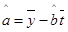 .
.
设函数
(Ⅰ)求函数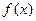 的极大值;
的极大值;
(Ⅱ)若 时,恒有
时,恒有 成立(其中
成立(其中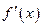 是函数
是函数 的导函数),试确定实数
的导函数),试确定实数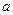 的取值范围.
的取值范围.
已知椭圆 过点
过点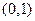 ,且离心率为
,且离心率为 .
.
(1)求椭圆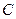 的方程;
的方程;
(2)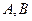 为椭圆
为椭圆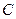 的左右顶点,直线
的左右顶点,直线 与
与 轴交于点
轴交于点 ,点
,点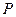 是椭圆
是椭圆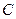 上异于
上异于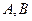 的动点,直线
的动点,直线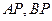 分别交直线
分别交直线 于
于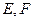 两点.证明:当点
两点.证明:当点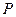 在椭圆
在椭圆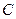 上运动时,
上运动时, 恒为定值.
恒为定值.
如图,在三棱柱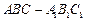 中,
中,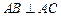 ,顶点
,顶点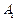 在底面
在底面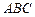 上的射影恰为点
上的射影恰为点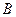 ,且
,且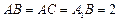 .
.
(Ⅰ)证明:平面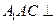 平面
平面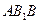 ;
;
(Ⅱ)求棱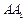 与
与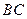 所成的角的大小;
所成的角的大小;
(Ⅲ)若点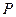 为
为 的中点,并求出二面角
的中点,并求出二面角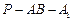 的平面角的余弦值.
的平面角的余弦值.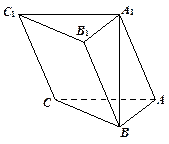
已知等比数列 的公比
的公比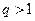 ,
, 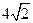 是
是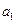 和
和 的一个等比中项,
的一个等比中项,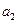 和
和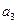 的等差中项为
的等差中项为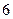 ,若数列
,若数列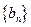 满足
满足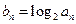 (
( ).
).
(Ⅰ)求数列 的通项公式;(Ⅱ)求数列
的通项公式;(Ⅱ)求数列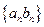 的前
的前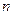 项和
项和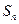 .
.
已知向量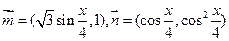 ,
,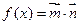 .
.
(I)若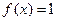 ,求
,求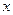 的值;
的值;
(II)在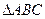 中,角
中,角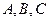 的对边分别是
的对边分别是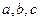 ,且满足
,且满足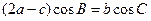 ,求函数
,求函数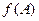 的取值范围
的取值范围