某射击小组有甲、乙两名射手,甲的命中率为
 ,乙的命中率为
,乙的命中率为 ,在射击比武活动中每人射击两发子弹则完成一次检测,在一次检测中,若两人命中次数相等且都不少于一发,则称该射击小组为“先进和谐组”.(Ⅰ)若
,在射击比武活动中每人射击两发子弹则完成一次检测,在一次检测中,若两人命中次数相等且都不少于一发,则称该射击小组为“先进和谐组”.(Ⅰ)若
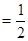 ,求该小组在一次检测中荣获“先进和谐组”的概率;(Ⅱ)计划在2011年每月进行1次检测,设这12次检测中该小组获得“先进和谐组”的次数为
,求该小组在一次检测中荣获“先进和谐组”的概率;(Ⅱ)计划在2011年每月进行1次检测,设这12次检测中该小组获得“先进和谐组”的次数为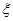 , 如果
, 如果 ,求
,求 的取值范围.
的取值范围.
(本小题满分12分)
已知实数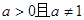 ,命题
,命题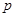 :
: 在区间
在区间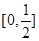 上为减函数;命题
上为减函数;命题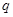 :方程
:方程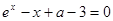 在
在 有解。若
有解。若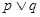 为真,
为真,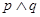 为假,求实数
为假,求实数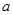 的取值范围。
的取值范围。
(本小题满分12分)
在△ABC中,设角A、B、C的对边分别为a、b、c,且 .
.
(1)求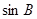 的值;
的值;
(2)若 ,且
,且 ,求△ABC的面积.
,求△ABC的面积.
(本小题满分14分)
已知函数 在
在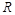 上有定义,对任意实数
上有定义,对任意实数 和任意实数
和任意实数 ,都有
,都有 .
.
(Ⅰ)证明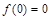 ;
;
(Ⅱ)证明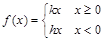 (其中k和h均为常数);
(其中k和h均为常数);
(Ⅲ)当(Ⅱ)中 的时,设
的时,设 ,讨论
,讨论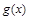 在
在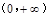 内的单调性.
内的单调性.
(本小题满分12分)
如图,在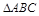 中,设
中,设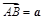 ,
, ,
, 的中点为
的中点为 ,
, 的中点为
的中点为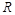 ,
, 的中点恰为
的中点恰为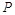 .
.
(Ⅰ)若 ,求
,求 和
和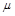 的值;
的值;
(Ⅱ)以 ,
,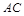 为邻边,
为邻边,  为对角线,作平行四边形
为对角线,作平行四边形 ,
,
求平行四边形 和三角形
和三角形 的面积之比
的面积之比 .
.
(本小题满分12分)
已知 的内角
的内角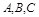 所对的边分别是
所对的边分别是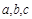 ,设向量
,设向量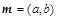 ,
,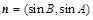 ,
, .
.
(Ⅰ)若 //
// ,求证:
,求证: 为等腰三角形;
为等腰三角形;
(Ⅱ)若 ⊥
⊥ ,边长
,边长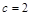 ,
, ,求
,求 的面积.
的面积.