如图,我市有一个健身公园,由一个直径为2km的半圆和一个以 为斜边的等腰直角三角形
为斜边的等腰直角三角形 构成,其中
构成,其中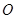 为
为 的中点.现准备在公园里建设一条四边形健康跑道
的中点.现准备在公园里建设一条四边形健康跑道 ,按实际需要,四边形
,按实际需要,四边形 的两个顶点
的两个顶点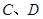 分别在线段
分别在线段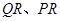 上,另外两个顶点
上,另外两个顶点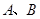 在半圆上,
在半圆上,  ,且
,且 间的距离为1km.设四边形
间的距离为1km.设四边形 的周长为
的周长为 km.
km.
(1)若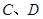 分别为
分别为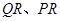 的中点,求
的中点,求 长;
长;
(2)求周长 的最大值.
的最大值.
下表提供了某厂节能降耗技术发行后,生产甲产品过程中记录的产量 (吨)与相应的生产能耗y(吨标准煤)的几组对应数据.
(吨)与相应的生产能耗y(吨标准煤)的几组对应数据.
| x |
3 |
4 |
5 |
6 |
| y |
2.5 |
3 |
4 |
4.5 |
(1)求线性回归方程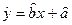 所表示的直线必经过的点;
所表示的直线必经过的点;
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程 ;
;
并预测生产1000吨甲产品的生产能耗多少吨标准煤?
(参考: )
)
(本小题满分14分)
已知数列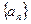 中,
中,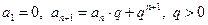 ,
,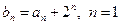 ,2,3,…
,2,3,…
(I)求证数列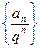 是等差数列;
是等差数列;
(II)试比较 的大小;
的大小;
(III)求正整数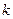 ,使得对于任意的正整数
,使得对于任意的正整数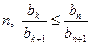 恒成立。
恒成立。
(本小题满分14分)
设函数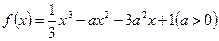 。
。
(I)求函数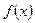 的单调区间、极大值和极小值。
的单调区间、极大值和极小值。
(II)若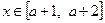 时,恒有
时,恒有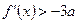 ,求实数
,求实数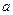 的取值范围。
的取值范围。
(本小题满分13分)
已知等差数列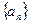 的前
的前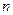 项和为
项和为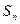 ,已知
,已知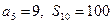 。
。
(I)求通项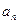 ;
;
(II)记数列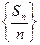 的前
的前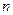 项和为
项和为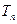 ,数列
,数列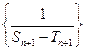 的前
的前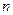 项和为
项和为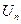 ,求证:
,求证: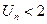 。
。
(本小题满分13分)
如图,要设计一张矩形广告,该广告含有大小相等的左右两个矩形栏目(即图中阴影部分),这两栏的面积之和为 四周空白的宽度为
四周空白的宽度为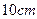 ,两栏之间的中缝空白宽度为
,两栏之间的中缝空白宽度为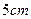 ,怎样确定广告的高与宽的尺寸(单位:cm),能使矩形广告面积最小?
,怎样确定广告的高与宽的尺寸(单位:cm),能使矩形广告面积最小?