(本小题满分12分)
如图,某建筑物的基本单元可近似地按以下方法构作:先在地平面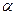 内作菱形ABCD,边长为1,∠BAD=60°,再在
内作菱形ABCD,边长为1,∠BAD=60°,再在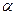 的上侧,分别以△
的上侧,分别以△ 与△
与△ 为底面安装上相同的正棱锥P-ABD与Q-CBD,∠APB=90°.
为底面安装上相同的正棱锥P-ABD与Q-CBD,∠APB=90°.
(1)求证:PQ⊥BD;
(2)求点P到平面QBD的距离.
对划艇运动员甲、乙二人在相同条件下进行6次测试,测得他们的速度的数据
如下:甲:27,38,30,37,35,31
乙:33,29,38,34,28,36
根据以上数据判断,谁更优秀。
用辗转相除法求5280与12155的最大公约数。
如图,在长方体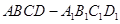 中,
中,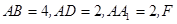 是棱
是棱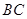 的中点,点
的中点,点 在棱
在棱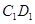 上,且
上,且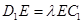 (
(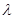 为实数).
为实数).
(1)当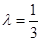 时,求直线
时,求直线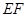 与平面
与平面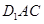 所成角的正弦值的大小;
所成角的正弦值的大小;
(2)试问:直线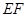 与直线
与直线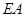 能否垂直?请说明理由.
能否垂直?请说明理由.
抛掷A,B,C三枚质地不均匀的纪念币,它们正面向上的概率如下表所示 ;
;
| 纪念币 |
A |
B |
C |
| 概率 |
 |
a |
a |
将这三枚纪念币同时抛掷一次,设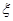 表示出现正面向上的纪念币的个数.
表示出现正面向上的纪念币的个数.
(1)求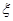 的分布列及数学期望;
的分布列及数学期望;
(2)在概率 中,若
中,若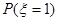 的值最大,求a的最大值
的值最大,求a的最大值
已知曲线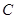 :
: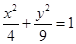 ,直线
,直线 :
: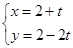 (
( 为参数).
为参数).
(1)写出曲线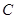 的参数方程,直线
的参数方程,直线 的普通方程;
的普通方程;
(2)过曲线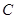 上任一点
上任一点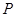 作与
作与 夹角为
夹角为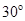 的直线,交
的直线,交 于点
于点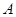 ,求
,求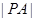 的最大值与最小值.
的最大值与最小值.