（本小题满分12分）学校为测评班级学生对任课教师的满意度，采用“100分制”打分的方式来计分．现从某班学生中随机抽取10名，以下茎叶图记录了他们对某教师的满意度分数（以十位数字为茎，个位数字为叶）：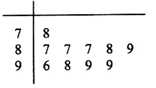
规定若满意度不低于98分，测评价该教师为“优秀”．
（Ⅰ）求从这10人中随机选取3人，至多有1人评价该教师是“优秀”的概率；
（Ⅱ）以这10人的样本数据来估计整个班级的总体数据，若从该班任选3人，
记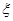
表示抽到评价该教师为“优秀”的人数，求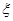的分布列及数学期望．
（本小题满分13分）已知函数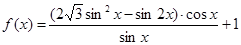
.
（1）求
的定义域及最小正周期；
（2）求在区间
上的最值.
（本小题满分12分）已知
, 
.
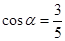求下列式子的值
（1）
；（2）
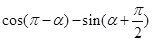（3）
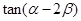
（本小题满分14分）已知数列
中，
，其前
项和
满足
．
（Ⅰ）求证：数列为等差数列，并求的通项公式；
（Ⅱ）设
，求数列
的前项和
；
（Ⅲ）设
（
为非零整数，
），是否存在确定的值，使得对任意，有
恒成立．若存在求出的值，若不存在说明理由。
（本小题满分13分）已知关于
的不等式
（1）若不等式的解集是
，求
的值；
（2）若
，求此不等式的解集．
（本小题满分12分）在一个月内分批购入每张价值为20元的书桌共36台，每批都购入x台（x是正整数），且每批均需付运费4元，储存购入的书桌一个月所付的保管费与每批购入书桌的总价值（不含运费）成正比，若每批购入4台，则该月需用去运费和保管费共52元，现在全月只有48元资金可以用于支付运费和保管费．
（1）求该月需用去的运费和保管费的总费用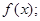
（2）能否恰当地安排每批进货的数量，使资金够用？写出你的结论，并说明理由．