设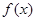 与
与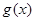 是定义在同一区间
是定义在同一区间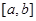 上的两个函数,若对任意的
上的两个函数,若对任意的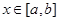 ,都有
,都有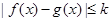 (
(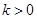 ),则称
),则称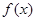 和
和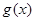 在
在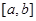 上是“
上是“ 度和谐函数”,
度和谐函数”,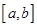 称为“
称为“ 度密切区间”,设
度密切区间”,设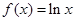 与
与 在
在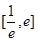 上是“
上是“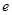 度和谐函数”,则
度和谐函数”,则 的取值范围是( )
的取值范围是( )
A. |
B. |
C.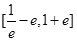 |
D.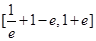 |
在锐角三角形中,a、b、c分别是内角A、B、C的对边,设B=2A,则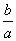 的取值范围是( )
的取值范围是( )
A.(-2,2) B.(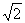
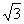 )
) C.(
C.(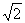 ,2) D.(0,2)
,2) D.(0,2)
在R上定义运算*:a*b=ab+2a+b,则满足x*(x-2)<0的实数x的取值范围为()
A.(0,2) B C.(-2,1) D.(-1,2)
C.(-2,1) D.(-1,2)
已知△ABC中,acosB=bcosA,则△ABC为( )
| A.等腰三角形 | B.直角三角形 |
| C.等腰或直角三角形 | D.钝角三角形 |
△ABC的内角A、B、C的对边分别为a、b、c.若a、b、c成等比数列,且c=2a,
则cosB等于
A. B.
B. C.
C. D.
D.
设 R且满足
R且满足 ,则
,则 的最小值等于 ( )
的最小值等于 ( )
A. |
B. |
C. |
D. |