(本小题满分12分)已知抛物线y2="2px" (p>0)上点T(3,t)到焦点F的距离为4.
(Ⅰ)求t,p的值;
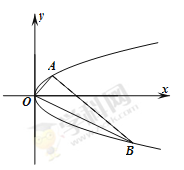
(Ⅱ)设A、B是抛物线上分别位于x轴两侧的两个动点,且 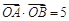 (其中 O为坐标原点).
(其中 O为坐标原点).
(ⅰ)求证:直线AB必过定点,并求出该定点P的坐标;
(ⅱ)过点P作AB的垂线与抛物线交于C、D两点,求四边形ACBD面积的最小值.
设常数
,函数
.
(1)若
,求函数
的反函数
;
(2)根据
的不同取值,讨论函数
的奇偶性,并说明理由.
底面边长为2的正三棱锥
,其表面展开图是三角形
,如图,求
的各边长及此三棱锥的体积
.
设函数
,其中
是
的导函数.
,
(1)求
的表达式;
(2)若
恒成立,求实数
的取值范围;
(3)设
,比较
与
的大小,并加以证明.
如图,曲线
由上半椭圆
和部分抛物线
连接而成,
的公共点为
,其中
的离心率为
.
(1)求
的值;
(2)过点
的直线
与
分别交于
(均异于点
),若
,求直线
的方程.
在一块耕地上种植一种作物,每季种植成本为1000元,此作物的市场价格和这块地上的产量均具有随机性,且互不影响,其具体情况如下表:
(1)设
表示在这块地上种植1季此作物的利润,求
的分布列;
(2)若在这块地上连续3季种植此作物,求这3季中至少有2季的利润不少于2000元的概率.