(本小题满分12分)已知椭圆C: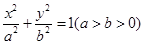 过点
过点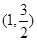 ,且椭圆C的离心率为
,且椭圆C的离心率为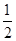 .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)若动点P在直线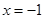 上,过P作直线交椭圆C于M,N两点,且P为线段MN中点,再过P作直线
上,过P作直线交椭圆C于M,N两点,且P为线段MN中点,再过P作直线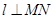 .证明:直线
.证明:直线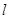 恒过定点,并求出该定点的坐标.
恒过定点,并求出该定点的坐标.
(Ⅰ)在等差数列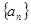 中,
中,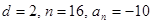 ,求
,求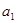 及
及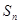 ;
;
(Ⅱ)在等比数列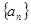 中,已知
中,已知 ,
,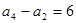 ,求
,求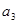 。
。
设数列 满足
满足 。
。
(1)求数列 的通项公式
的通项公式 ;
;
(2)令 ,求数列
,求数列 的前
的前 项和
项和 ;
;
 。
。
已知某地今年年初拥有居民住房的总面积为 (单位:m2),其中有部分旧住房需要拆除。当地有关部门决定每年以当年年初住房面积的10%建设新住房,同时也拆除面积为b(单位:m2)的旧住房。
(单位:m2),其中有部分旧住房需要拆除。当地有关部门决定每年以当年年初住房面积的10%建设新住房,同时也拆除面积为b(单位:m2)的旧住房。
(1)分别写出第一年末和第二年末的实际住房面积的表达式;
(2)如果第五年末该地的住房面积正好比今年年初的住房面积增加了30%,则每年拆除的旧住房面积b是多少?(计算时取1.15=1.6)
已知函数 ,
,
(1)解关于x的不等式f (x) > 0;
(2)若 上恒成立,求a的取值范围。
上恒成立,求a的取值范围。
已知数列 的通项
的通项 。
。
(1)当 为何值时,前
为何值时,前 项的和
项的和 有最小值,并求出这个最小值。
有最小值,并求出这个最小值。
(2)数列 前
前 项和为
项和为 ,求
,求 。
。