【原创】(本小题满分12分)已知F1、F2是椭圆 的左右焦点,离心率为
的左右焦点,离心率为 ,D是上顶点,C是右顶点,△CDF2的面积为
,D是上顶点,C是右顶点,△CDF2的面积为 .
.
(Ⅰ)求椭圆E的方程;
(Ⅱ)若动直线 与椭圆E相交于A、B求△AOB面积的最大值.
与椭圆E相交于A、B求△AOB面积的最大值.
(本小题满分10分)在锐角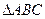 中,A、B、C三内角所对的边分别为a、b、c,
中,A、B、C三内角所对的边分别为a、b、c,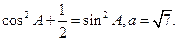
(1)若b=3,求c;
(2)求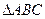 的面积的最大值。
的面积的最大值。
定义在R上的增函数y=f(x)对任意x,y∈R都有f(x+y)=f(x)+f(y).
(Ⅰ)求f (0)
(0)
(Ⅱ)求证f(x)为奇函数;
(Ⅲ)若f(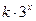 )+f(3
)+f(3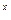 -9
-9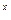 -2)<0对任意x∈R恒成立,求实数k的取值范围.
-2)<0对任意x∈R恒成立,求实数k的取值范围.
设二次函数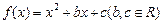 ,已知不论
,已知不论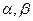 为何实数恒有
为何实数恒有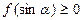 ,
,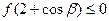
(1)求证: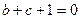 ;
;
( 2)求证:
2)求证: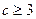 ;
;
(3)若函数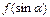 的最大值为8,求
的最大值为8,求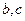 值.
值.
已知集合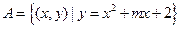 ,
,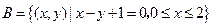 .
.
若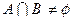 ,求实数
,求实数 的取值范围.
的取值范围.
如图,某污水处理厂要在一个矩形污水处理池(ABCD)的池底水平铺设污水净化管道(Rt∆FHE,H是直角顶点)来处理污水,管道越长,污水净化效果越好.设计要求管道的接口H是AB的中点,E,F分别落在线段BC,AD上.已知AB=20米,AD=10 米,记∠BHE=θ.
米,记∠BHE=θ.
(1)试将污水净化管道的长度L表示为θ的函数,并写出定义域;
(2)若sinθ+cosθ=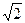 ,求此时管道的长度L;
,求此时管道的长度L;
(3)问:当θ取何值时,污水净化效果最好?
并求出此时管道的长度.