是否存在实数a,使函数 为奇函数,同时使函数
为奇函数,同时使函数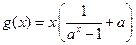 为偶函数,证明你的结论。
为偶函数,证明你的结论。
如图,在四棱锥 中,平面 , , , . .
(1)证明:
;
(2)求二面角
的大小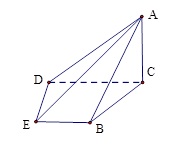
已知数列 和 满足 .若 为等比数列,且
(1)求
与
;
(2)设
。记数列
的前
项和为
.
(i)求
;
(ii)求正整数
,使得对任意
,均有
.
在 中,内角 所对的边分别为 .已知 .
(1)求角
的大小;
(2)若
,求
的面积.
已知函数
.已知函数
有两个零点
,且
.
(1)求
的取值范围;
(2)证明
随着
的减小而增大;
(3)证明
随着
的减小而增大.
已知 和 均为给定的大于1的自然数,设集合 ,集合 .
(Ⅰ)当 时,用列举法表示集合 ;
(Ⅱ)设 , ,其中 , .证明:若 ,则 .