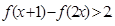已知椭圆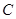 :
: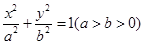 ,
,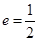 ,其中
,其中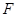 是椭圆的右焦点,焦距为
是椭圆的右焦点,焦距为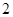 ,直线
,直线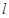 与椭圆
与椭圆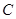 交于点
交于点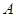 ,
,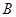 ,点
,点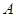 ,
,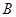 的中点横坐标为
的中点横坐标为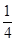 ,且
,且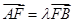 (其中
(其中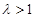 ).
).
(1)求椭圆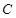 的标准方程;
的标准方程;
(2)求实数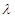 的值.
的值.
已知数列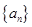 中的相邻两项
中的相邻两项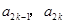 是关于
是关于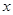 的方程
的方程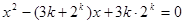 的两个根,且
的两个根,且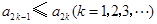 .
.
(I)求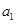 ,
,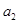 ,
,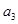 ,
,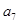 ;
;
(II)求数列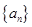 的前
的前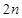 项和
项和 ;
;
(Ⅲ)记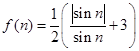 ,
,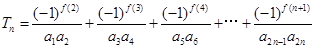 ,
,
求证: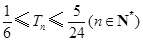 .
.
已知定义在R上的函数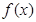 和数列
和数列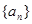 满足下列条件:
满足下列条件: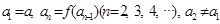 ,
,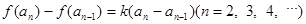 ,其中a为常数,k为非零常数.
,其中a为常数,k为非零常数.
(Ⅰ)令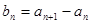
 ,证明数列
,证明数列 是等比数列;
是等比数列;
(Ⅱ)求数列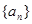 的通项公式;
的通项公式;
(Ⅲ)当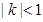 时,求
时,求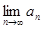 .
.
、设函数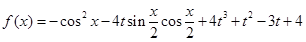 ,
,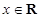 ,其中|t|≤1,将f(x)的最小值记为g(t).
,其中|t|≤1,将f(x)的最小值记为g(t).
(1)求g(t)的表达式;
(2)对于区间[-1,1]中的某个t,是否存在实数a,使得不等式g(t)≤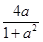 成立?如果存在,求出这样的a及其对应的t;如果不存在,请说明理由.
成立?如果存在,求出这样的a及其对应的t;如果不存在,请说明理由.
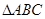 中,内角
中,内角 的对边分别是
的对边分别是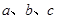 ,已知
,已知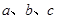 成等比数列,且
成等比数列,且
(Ⅰ)求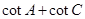 的值(Ⅱ)设
的值(Ⅱ)设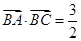 ,求
,求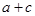 的值。
的值。
、设 是定义在
是定义在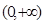 上的增函数,对任意
上的增函数,对任意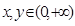 ,满足
,满足 。
。
(1)、求证:①当
(2)、若 ,解不等式
,解不等式