已知△ABC的三个内角A、B、C所对的边分别为a、b、c，向量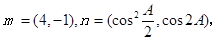
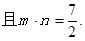
（Ⅰ）求角A的大小；
（Ⅱ）若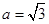
，试判断b·c取得最大值时△ABC形状.
已知函数f(x)＝ax3＋bx2＋cx在x＝±1处取得极值，且在x＝0处的切线的斜率为－3.
(1)求f(x)的解析式；
(2)若过点A(2，m)可作曲线y＝f(x)的三条切线，求实数m的取值范围．
已知幂函数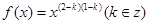
满足
。
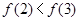（1）求实数k的值，并写出相应的函数
的解析式；
（2）对于（1）中的函数，试判断是否存在正数m，使函数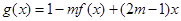
，在区间上的最大值为5。若存在，求出m的值；若不存在，请说明理由。
函数
是定义在
上的奇函数，且
。
（1）求实数a，b，并确定函数
的解析式；
（2）判断在（-1，1）上的单调性，并用定义证明你的结论；
（3）写出的单调减区间，并判断有无最大值或最小值？如有，写出最大值或最小值。（本小问不需要说明理由）
已知函数
（1）若函数
的图象经过P（3，4）点，求a的值；
（2）比较
大小，并写出比较过程；
（3）若
，求a的值.
的焦点为
，点
关于坐标原点对称，以
为焦点的椭圆
，过点
，过点
与椭圆
两点，且
，若
，求
的最小值。