已知:关于x的一元二次方程-x2+(m+1)x+(m+2)=0(m>0).
(1)求证:该方程有两个不相等的实数根;
(2)当抛物线y=-x2+(m+1)x+(m+2)经过点3,0),求该抛物线的表达式;
(3)在(2)的条件下,记抛物线y=-x2+(m+1)x+(m+2)在第一象限之间的部分为图象G,如果直线
y=k(x+1)+4与图象G有公共点,请结合函数的图象,求直线y=k(x+1)+4与y轴交点的纵坐标t的取值
范围.
解方程组:(本题共8分,每题4分).
(1)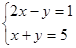
(2)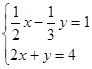 ①②
①②
因式分解:(本题共12分,每题4分).
(1)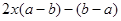
(2)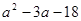
(3)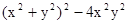
计算或化简求值:(本题共12分,每题4分).
(1)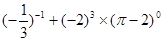
(2)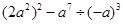
(3)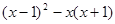
如图.等腰直角三角形ABC中,∠A=90°,P为BC的中点,小明拿着含45°角的透明三角形,使45°角的顶点落在点P,且绕P旋转.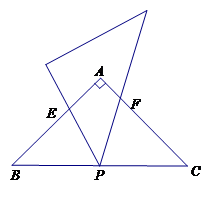
(1)如图①:当三角板的两边分别AB、AC交于E、F点时,试说明△BPE∽△CFP.
(2)将三角板绕点P旋转到图②,三角板两边分别交BA延长线和边AC于点EF.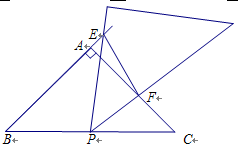
探究1:△BPE与△CFP.还相似吗?(只需写结论)
探究2:连接EF,△BPE与△EFP是否相似?请说明理由.
如图所示,已知正方形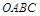 的面积为9 ,点
的面积为9 ,点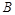 在函数
在函数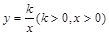 的图象上,点
的图象上,点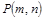 (
(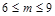 )是函数
)是函数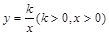 的图象上动点,过点
的图象上动点,过点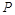 分别作
分别作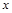 轴、
轴、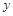 轴的垂线,垂足分别为
轴的垂线,垂足分别为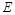 、
、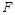 ,若设矩形
,若设矩形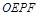 和正方形
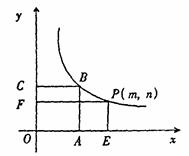
和正方形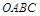 不重合的两部分的面积和为
不重合的两部分的面积和为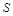 。
。
(1)求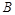 点坐标和
点坐标和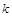 的值;(2)写出
的值;(2)写出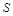 关于
关于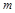 的函数关系和
的函数关系和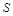 的最大值。
的最大值。