如图，已知抛物线
过点A（6，0），B（－2，0），C（0，－3）．
（1）求此抛物线的解析式；
（2）若点H是该抛物线第四象限的任意一点，求四边形OCHA的最大面积；
（3）若点Q在
轴上，点G为该抛物线的顶点，且∠QGA=45º，求点Q的坐标．
下列方程中哪些是二元一次方程？
（1）8x－y＝y；（2）xy＝3；（3）2x2－y＝9；（4）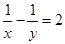
；（5）m＝2n．
如图所示，△ABC中的点A（－3，－1），B（－2，－3），C（－1，－2）是分别通过△A′B′C′中的点A′，B′，C′向下平移2个单位长度，又向左平移3个单位长度得到的，试画出△A′B′C′的位置．
如图所示，某校的校门口，教学楼，图书馆和实验楼分别位于一个长方形的四个顶点处，请你选择适当的位置作为坐标原点，建立平面直角坐标系并描述图中的各个位置．
如图，若观测点的高度为h，观测者视线能达到的最远距离为d，则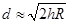
，其中R是地球半径(通常取6400km)．
(1)小丽站在海边一块岩石上，眼睛离地面的高度为20m，此时小丽视线能达到的最远距离为多少千米？
(2)已知泰山到海边的最近距离是216000m，泰山的海拔高度为1545m，利用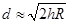计算，判断站在泰山之巅能否看到大海．
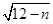为一个整数，试求出自然数n的值．