如图，若观测点的高度为h，观测者视线能达到的最远距离为d，则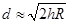
，其中R是地球半径(通常取6400km)．
(1)小丽站在海边一块岩石上，眼睛离地面的高度为20m，此时小丽视线能达到的最远距离为多少千米？
(2)已知泰山到海边的最近距离是216000m，泰山的海拔高度为1545m，利用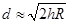计算，判断站在泰山之巅能否看到大海．
某市气象局统计了5月1日至8日中午12时的气温（单位： ，整理后分别绘制成如图所示的两幅统计图．
根据图中给出的信息，解答下列问题：
（1）该市5月1日至8日中午时气温的平均数是 ，中位数是 ；
（2）求扇形统计图中扇形 的圆心角的度数；
（3）现从该市5月1日至5日的5天中，随机抽取2天，求恰好抽到2天中午12时的气温均低于 的概率．
化简： ．
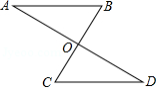
如图， ， 和 相交于点 ， ．求证： ．
如图，抛物线 的图象过点 、 、 ．
（1）求抛物线的解析式；
（2）在抛物线的对称轴上是否存在一点 ，使得 的周长最小，若存在，请求出点 的坐标及 的周长；若不存在，请说明理由；
（3）在（2）的条件下，在 轴上方的抛物线上是否存在点 （不与 点重合），使得 ？若存在，请求出点 的坐标；若不存在，请说明理由．
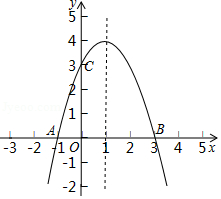
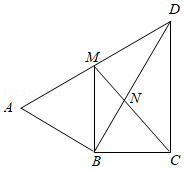
如图， ， 平分 ，过点 作 交 于 ．连接 交 于 ．
（1）求证： ；
（2）若 ， ，求 的长．
