在一个不透明的布袋里装有4个标有1,2,3,4的小球,它们的形状、大
小、质地完全相同,李晓同学从布袋里随机取出一个小球,记下数字为x,张丹同学在剩下的3个
小球中随机取出一个小球,记下数字为y,这样确定了点Q的坐标(x,y).
(1)画树状图或列表,写出点Q所有可能的坐标;
(2)求点Q(x,y)在函数y=﹣x+6图象上的概率.
如图:已知二次函数的图象经过点A(-1,0),B(3,0),C(0,-5),
(1)试确定此二次函数的解析式;
(2)点P是抛物线对称轴上的一个动点,是否存在点P,使PB+PC的值最小,如果存在,请求出点P的坐标,如果不存在,请说明理由。
六一儿童节,某学习用品销售商店推出两种优惠方法:①购1个书包,赠送1支水性笔;②购书包和水性笔一律按9折优惠。其中,书包每个定价20元,水性笔每支定价5元。小丽和同学需买4个书包,水性笔若干支(不少于4支)。
(1)分别写出两种优惠方法购买费用 (元)与所买水性笔支数
(元)与所买水性笔支数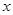 (支)的函数解析式(请化简函数解析式);
(支)的函数解析式(请化简函数解析式);
(2)对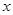 的取值情况进行分析,说明按哪种优惠方法购买比较便宜。
的取值情况进行分析,说明按哪种优惠方法购买比较便宜。
如图,杂技团进行杂技表演,演员从跷跷板右端A处弹跳到人梯顶端椅子B处,其身体(看成一点)的路线是抛物线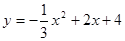 的一部分。
的一部分。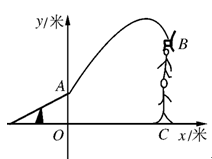
(1)求演员弹跳离地面的最大高度;
(2)已知在一次表演中,人梯高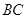 =4米,人梯到起跳点
=4米,人梯到起跳点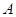 的水平距离是6米,问这次表演是否成功?请说明理由。
的水平距离是6米,问这次表演是否成功?请说明理由。
经统计分析,南博会期间,昆明环湖东路上的车流速度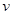 (千米/小时)是车流密度
(千米/小时)是车流密度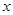 (辆/千米)的一次函数。当车流密度为20辆/千米时,车流速度为80千米/小时;当车流密度达到220辆/千米时,造成堵塞,此时车流速度为0千米/小时。求大桥上车流密度为100辆/千米时的车流速度。
(辆/千米)的一次函数。当车流密度为20辆/千米时,车流速度为80千米/小时;当车流密度达到220辆/千米时,造成堵塞,此时车流速度为0千米/小时。求大桥上车流密度为100辆/千米时的车流速度。
某公司招聘职员,对甲、乙两位候选人进行了面试和笔试,面试中包括形体和口才,笔试中包括专业水平和创造能力考察,他们的成绩(百分制)如下表: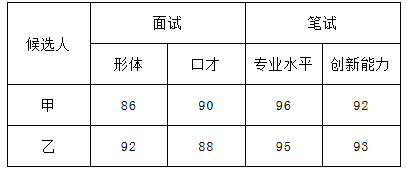
若公司根据经营性质和岗位要求认为:形体、口才、专业水平、创新能力按照1:2:1:2的比确定,请计算甲、乙两人各自的平均成绩,看看谁将被录取?