(本小题满分10分)
已知在平面直角坐标系中,点A,B表示两个大型综合商场,坐标分别为A(2,-5),B(5,1) x轴,y轴分别表示庆春路和延安路,请在同一个坐标系内画出满足下列条件的点(保留画图痕迹),并求出点C的坐标 
(1)现打算在延安路上建一个地铁出口站C,使得它到两个商场的直线距离最小;
(2)小敏到庆春路上的书店D买书,它到A商场的距离与它到B商场的直线距离之差达到最大
图是某单位职工的年龄(取正整数)(单位:岁)的频数分布直方图,根据图形提供的信息回答下列问题:
(1)该单位在哪个年龄段的人数最多?哪个年龄段的人数最少?各是多少?
(2)36~38岁(不含38岁)的职工有多少人?
(3)该单位职工共有多少人?
(4)38~42岁(不含42岁)的职工人数占职工总人数的百分比是多少?
林城市对教师试卷讲评课中学生参与的深度与广度进行评价,其评价项目为主动质疑、独立思考、专注听讲、讲解题目四项.评价组随机抽取了若干名初中学生的参与情况,绘制了如下两幅不完整的统计图,请根据图中所给信息解答下列问题:
(1)在这次评价中,一共抽查了________名学生.
(2)请将条形图补充完整.
(3)如果全市有16万名初中学生,那么在试卷讲评课中,“独立思考”的学生约有多少万人?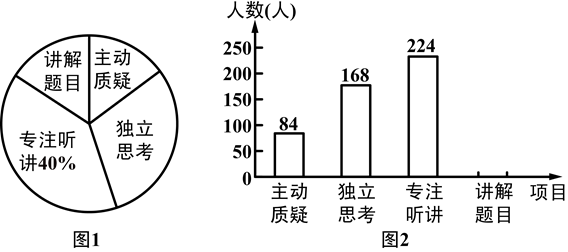
制作适当的统计图表示下列数据:
对某城市家庭人口数的一次统计结果表明:2口人家占23%,3口人家占42%,4口人家占21%,5口人家占9%,6口人家占3%,其他占2%.
某市有6500名九年级学生参加毕业考试,为了了解这些学生毕业考试的数学成绩,从6500份数学答卷中随机抽取了300份进行统计分析.在这个问题中,总体、个体、样本及样本容量各指什么?
下列调查中,哪些适合抽样抽查?哪些适合全面调查?为什么?
(1)某工厂准备对一批即将出厂的饮料中含有细菌总数的情况进行调查;(2)小明准备对全班同学喜欢球类运动的情况进行调查;(3)了解全市七年级同学的视力情况;(4)某农田保护区准备对区内的水稻秧苗的高度进行调查.