图是某单位职工的年龄(取正整数)(单位:岁)的频数分布直方图,根据图形提供的信息回答下列问题:
(1)该单位在哪个年龄段的人数最多?哪个年龄段的人数最少?各是多少?
(2)36~38岁(不含38岁)的职工有多少人?
(3)该单位职工共有多少人?
(4)38~42岁(不含42岁)的职工人数占职工总人数的百分比是多少?
在边长为16cm的正方形纸片的四个角各剪去一个同样大小的正方形,折成一个无盖的长方体。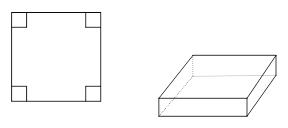
(1)如果剪去的小正方形的边长为xcm,请用x来表示这个无盖长方体的容积;
(2)当剪去的小正方体的边长x的值分别为3cm和3.5cm时,比较折成的无盖长方体的容积的大小。
已知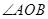 是一个直角,在角的内部作射线
是一个直角,在角的内部作射线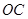 ,再分别作
,再分别作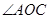 和
和 的平分线
的平分线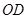 、
、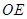 .
.
(1)如图①,当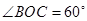 时,则求
时,则求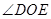 的度数;
的度数;
(2)如图②,当射线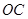 在
在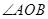 内绕
内绕 点旋转时,
点旋转时,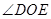 的大小是否发生变化?若变化,说明理由;若不变,求
的大小是否发生变化?若变化,说明理由;若不变,求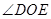 的度数.
的度数.
“老牛:累死我了!
小马:你还累?这么大的个,才比我多驮了2个。
老牛:哼,我从你背上拿来1个,我的包裹数就是你的2倍!
小马:真的?!”
根据老牛和小马的对话,你能求出它们各驮了多少个包裹吗?
(1)在如图所示的方格纸中,点P是∠AOB的边OB上的一点,不用量角器与三角尺,仅用直尺,完成下列各题: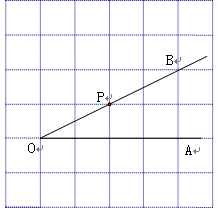
①过点P画OB的垂线,交OA于点C ;
②过点P画OA的垂线,垂足为H;
(2)在上图中线段PH的长度是点P到 的距离,线段 的长度是点C到直线OB的距离.PC、PH、OC这三条线段大小关系是 .(用“<”号连接)
(1)化简求值: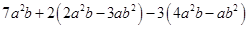 ,其中
,其中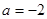 、
、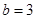
(2)已知关于x的方程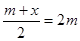 的解与方程2x-1=3的解相同,求m的值
的解与方程2x-1=3的解相同,求m的值