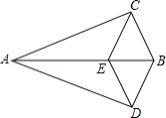
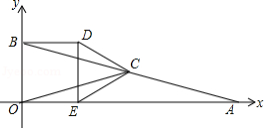
如图,在平面直角坐标系中, 的顶点 为坐标原点,点 的坐标为 ,点 的坐标为 ,点 为边 的中点,正方形 的顶点 在 轴的正半轴上,连接 , , .
(1)线段 的长为 ;
(2)求证: ;
(3)将正方形 沿 轴正方向平移得到正方形 ,其中点 , , , 的对应点分别为点 , , , ,连接 , ,设点 的坐标为 ,其中 ,△ 的面积为 .
①当 时,请直接写出 与 之间的函数表达式;
②在平移过程中,当 时,请直接写出 的值.
倡导健康生活,推进全民健身,某社区要购进 , 两种型号的健身器材若干套, , 两种型号健身器材的购买单价分别为每套310元,460元,且每种型号健身器材必须整套购买.
(1)若购买 , 两种型号的健身器材共50套,且恰好支出20000元,求 , 两种型号健身器材各购买多少套?
(2)若购买 , 两种型号的健身器材共50套,且支出不超过18000元,求 种型号健身器材至少要购买多少套?
如图,在 中,以 为直径的 分别与 , 相交于点 , , ,过点 作 的切线交边 于点 .
(1)求证: ;
(2)若 的半径为5, ,求 的长(结果保留 .

我市某中学决定在学生中开展丢沙包、打篮球、跳大绳和踢毽球四种项目的活动,为了解学生对四种项目的喜欢情况,随机调查了该校 名学生最喜欢的一种项目(每名学生必选且只能选择四种活动项目的一种),并将调查结果绘制成如下的不完整的统计图表:
学生最喜欢的活动项目的人数统计表
|
项目 |
学生数(名 |
百分比 |
|
丢沙包 |
20 |
|
|
打篮球 |
60 |
|
|
跳大绳 |
|
|
|
踢毽球 |
40 |
|
根据图表中提供的信息,解答下列问题:
(1) , , ;
(2)请根据以上信息直接补全条形统计图;
(3)根据抽样调查结果,请你估计该校2000名学生中有多少名学生最喜欢跳大绳.

如图, ,点 在边 上, ,连接 .求证:
(1) ;
(2)四边形 是菱形.