(年河北省13分)某景区的环形路是边长为800米的正方形ABCD,如图,现有1号,2号两游览车分别从出口A和经典C同时出发,1号车顺时针,2号车逆时针沿环形路连续循环行驶,供游客随时乘车(上,下车的时间忽略不计),两车的速度均为200米/分.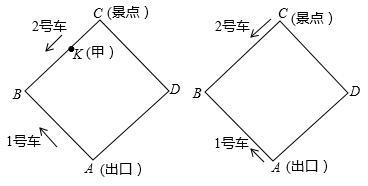
探究:设行驶时间为t分
(1)当0≤t≤s时,分别写出1号车,2号车在左半环线离出口A的路程y1,y2(米)与t的函数关系式,并求出当两车相距的路程是400米时t的值;
(2)t为何值时,1号车第三次恰好经过点C?,并直接写出这一段时间内它与2号车相遇过的次数.
发现:如图,游客甲在BC上一点K(不与点B,C重合)处候车,准备乘车到出口A,设CK=x米.
情况一:若他刚好错过2号车,便搭乘即将到来的1号车;
情况二:若他刚好错过1号车,便搭乘即将到来的2号车;
比较哪种情况用时较多?(含候车时间)
决策:已知游客乙在DA上从D向出口A走去,步行的速度是50米/分,当行进到DA上一点P(不与D,A重合)时,刚好与2号车相遇.
(1)他发现,乘1号车会比乘2号车到出口A用时少,请你简要说明理由;
(2)设PA=s(0<s<800)米,若他想尽快到达出口A,根据s的大小,在等候乘1号车还是步行这两种方式中,他该如何选择?
如图所示,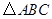 是直角三角形,
是直角三角形,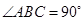 ,以
,以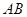 为直径的⊙O交
为直径的⊙O交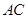 于点
于点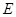 ,点
,点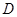 是
是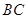 边的中点,连结
边的中点,连结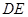 .
.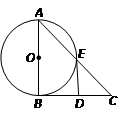
求证:
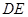 与⊙O相切
与⊙O相切若⊙O的半径为
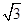 ,
,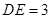 ,求
,求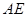 .
.
大家一定熟知杨辉三角(Ⅰ),观察下列等式(Ⅱ)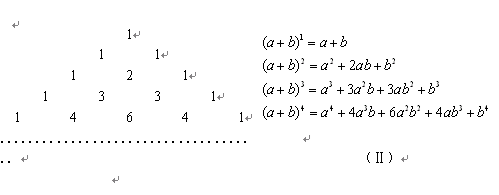
根据前面各式规律,则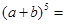 .
.
已知如图,矩形OABC的长OA= ,宽OC=1,
,宽OC=1,
将△AOC沿AC翻折得△APC.
求∠PCB的度数
若P,A两点在抛物线y=-
 x2+bx+c上,求b,c的值,并说明点C在此抛物线上;
x2+bx+c上,求b,c的值,并说明点C在此抛物线上;(2)中的抛物线与矩形OABC边CB相交于点D,与x轴相交于另外一点E,若点M是x轴上的点,N是y轴上的点,以点E、M、D、N为顶点的四边形是平行四边形,试求点M、N的坐标.
如图,抛物线 (a
(a 0)与反比例函数
0)与反比例函数 的图像相交于点A,B. 已知点A的坐标为(1,4),点B(t,q)在第三象限内,且△AOB的面积为3(O为坐标原点)
的图像相交于点A,B. 已知点A的坐标为(1,4),点B(t,q)在第三象限内,且△AOB的面积为3(O为坐标原点)
求反比例函数的解析式
用含t的代数式表示直线AB的解析式;
求抛物线的解析式;
过抛物线上点A作直线AC∥x轴,交抛物线于另一点C,把△AOB绕点O逆时针旋转90º,请在图②中画出旋转后的三角形,并直接写出所有满足△EOC∽△AOB的点E的坐标.
如图1,在 中,
中, ,
, ,
, ,另有一等腰梯形
,另有一等腰梯形 (
( )的底边
)的底边 与
与 重合,两腰分别落在AB、AC上,且G、F分别是AB、AC的中点.
重合,两腰分别落在AB、AC上,且G、F分别是AB、AC的中点.
直接写出△AGF与△ABC的面积的比值;
操作:固定
 ,将等腰梯形
,将等腰梯形 以每秒1个单位的速度沿
以每秒1个单位的速度沿 方向向右运动,直到点
方向向右运动,直到点 与点
与点 重合时停止.设运动时间为
重合时停止.设运动时间为 秒,运动后的等腰梯形为
秒,运动后的等腰梯形为 (如图2).
(如图2).
①探究1:在运动过程中,四边形 能否是菱形?若能,请求出此时
能否是菱形?若能,请求出此时 的值;若不能,请说明理由.
的值;若不能,请说明理由.
②探究2:设在运动过程中 与等腰梯形
与等腰梯形 重叠部分的面积为
重叠部分的面积为 ,求
,求 与
与 的函数关系式.
的函数关系式.