(年新疆乌鲁木齐12分)某公司销售一种进价为20元/个的计算机,其销售量y(万个)与销售价格x(元/个)的变化如下表:
| 价格x(元/个) |
… |
30 |
40 |
50 |
60 |
… |
| 销售量y(万个) |
… |
5 |
4 |
3 |
2 |
… |
同时,销售过程中的其他开支(不含造价)总计40万元.
(1)观察并分析表中的y与x之间的对应关系,用所学过的一次函数,反比例函数或二次函数的有关知识写出y(万个)与x(元/个)的函数解析式.
(2)求出该公司销售这种计算器的净得利润z(万个)与销售价格x(元/个)的函数解析式,销售价格定为多少元时净得利润最大,最大值是多少?
(3)该公司要求净得利润不能低于40万元,请写出销售价格x(元/个)的取值范围,若还需考虑销售量尽可能大,销售价格应定为多少元?
△ABC在直角坐标系中的位置如图所示,直线l经过点(-1,0),并且与y轴平行.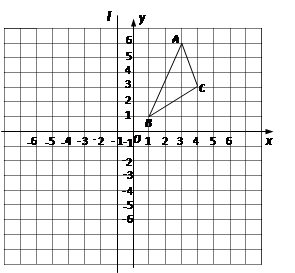
①将△ABC绕坐标原点O顺时针旋转90°得到△A1B1C1,在图中画出△A1B1C1;
②求出由点C运动到点C1所经过的路径的长.①△A2B2C2与△ABC关于直线l对称,画出△A2B2C2,并写出△A2B2C2三个顶点的
坐标;②观察△ABC与△A2B2C2对应点坐标之间的关系,写出直角坐标系中任意一点P(a,b)
关于直线l的对称点的坐标:__________.
如图,小明同学在操场上的A处放风筝,风筝起飞后到达C处,此时,在AQ延长线上B处的小亮同学,发现自己的位置与风筝和旗杆PQ的顶点P在同一直线上.已知旗杆PQ高为10m,若在B处测得旗杆顶点P的仰角为30°,A处测得点P
的仰角为45°,试求A、B之间的距离;此时,在A处又测得风筝的仰角为75°,若绳子AC在空中视为一条线段,绳子
AC的长约为多少?(结果可保留根号)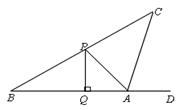
如图,用总长度为12米的不锈钢材料设计成外观为矩形的框架.当竖档AB为多少时,矩形框架ABCD的面积为3平方米?(题中的不锈钢材料总长度指图中所有黑线的长度和,所有横档和竖档分别与AD、AB平行)
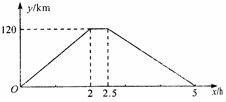
在一次运输任务中,一辆汽车将一批货物从甲地运往乙地,到达乙地卸货后返回.设汽车从甲地出发x(h)时,汽车与甲地的距离为y(km),y与x的函数关系如图所示.
根据图像信息,解答下列问题:这辆汽车的往、返速度是否相同?请说明理由;
求返程中y与x之间的函数表达式;
求这辆汽车从甲地出发4h时与甲地的距离.
小明与小红共同发明了一种“字母棋”,进行比胜负的游戏.他们用三种字母做成5只棋子(棋子除字母外其它均相同),其中A棋1只,B棋2只,C棋2只.
“字母棋”的游戏规则为:
随机从5只棋子中摸出两只棋子,若摸到A棋,则小明胜;若摸到两只相同的棋子,则小红胜.其余情况则为平局.
你认为这个游戏公平吗?请说明理由,若不公平请修改游戏规则使游戏公平.