（年黑龙江牡丹江农垦10分）某体育用品商店试销一款成本为50元的排球，规定试销期间单价不低于成本价，且获利不得高于40%．经试销发现，销售量y（个）与销售单价x（元）之间满足如图所示的一次函数关系．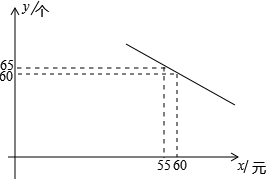
（1）试确定y与x之间的函数关系式；
（2）若该体育用品商店试销的这款排球所获得的利润Q元，试写出利润Q（元）与销售单价x（元）之间的函数关系式；当试销单价定为多少元时，该商店可获最大利润？最大利润是多少元？
（3）若该商店试销这款排球所获得的利润不低于600元，请确定销售单价x的取值范围．
已知a、b是方程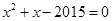
的两个实数根，求：
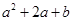的值．
如图，在建立了平面直角坐标系的正方形网格中，A（2，2），B（1，0），C（3，1）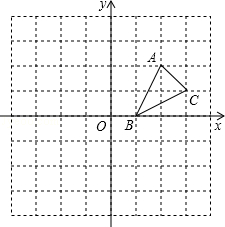
（1）画出ΔABC关于x轴对称的ΔA1B1C1．
（2）画出将ΔABC绕点B逆时针旋转900，所得的ΔA2B2C2．
（3）直接写出A2点的坐标．
解方程：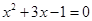
某商店经营一批进价每件为2元的小商品，在市场营销的过程中发现：如果该商品按每件最低价3元销售，日销售量为18件，如果单价每提高1元，日销售量就减少2件．设销售单价为x（元），日销售量为y（件）．
（1）写出日销售量y（件）与销售单价x（元）之间的函数关系式；
（2）设日销售的毛利润（毛利润=销售总额-总进价）为P（元），求出毛利润P（元）与销售单价x（元）之间的函数关系式；
（3）在下图所示的坐标系中画出P关于x的函数图象的草图，并标出顶点的坐标；
（4）观察图象，说出当销售单价为多少元时，日销售的毛利润最高？是多少？
如图，梯形ABCD中，AB∥CD，且AB=2CD，E，F分别是AB，BC的中点。EF与BD相交于点M．
（1）求证：△EDM∽△FBM；
（2）若DB=9，求BM．