(年广东广州14分)已知平面直角坐标系中两定点A(﹣1,0)、B(4,0),抛物线y=ax2+bx﹣2(a≠0)过点A,B,顶点为C,点P(m,n)(n<0)为抛物线上一点.
(1)求抛物线的解析式和顶点C的坐标;
(2)当∠APB为钝角时,求m的取值范围;
(3)若m> ,当∠APB为直角时,将该抛物线向左或向右平移t(0<t<
,当∠APB为直角时,将该抛物线向左或向右平移t(0<t<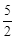 )个单位,点C、P平移后对应的点分别记为C′、P′,是否存在t,使得首尾依次连接A、B、P′、C′所构成的多边形的周长最短?若存在,求t的值并说明抛物线平移的方向;若不存在,请说明理由.
)个单位,点C、P平移后对应的点分别记为C′、P′,是否存在t,使得首尾依次连接A、B、P′、C′所构成的多边形的周长最短?若存在,求t的值并说明抛物线平移的方向;若不存在,请说明理由.
某书店举行图书促销会,每位促销人员以销售50本为基准,超过记为正,不足的记为负,其中10名促销人员的销售结果如下(单位:本):
4,2,3,-7,-3,-8,3,4,8,-1.
(1)这组促销人员的总销售量超过还是不足总销售基准?相差多少?
(2)如销售图书每本的利润为2.7元,此次促销会所得总利润为多少元?(结果保留整数)
化简:
(1) (2)
(2)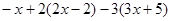
某家电生产企业根据市场调查分析,决定调整新产品方案,准备每周(按120个工时计算)生产空调、冰箱、彩电共360台,且空调至少生产60台.设生产彩电x台,生产冰箱y台.已知生产这些家电新产品每台所需工时和每台产值如下表:
| 家电名称 |
彩电 |
冰箱 |
空调 |
| 工时 |
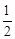 |
 |
 |
| 产值(千元) |
4 |
3 |
2 |
(1)用含x,y的式子表示生产空调的台数;
(2)求出y与x之间的函数关系式;
(3)每周应生产彩电、冰箱、空调各多少台,才能使产值最高,最高产值是多少千元?
小明一家利用元旦三天驾车到某景点旅游.小汽车出发前油箱有油36L,行驶若干小时后,途中在加油站加油若干升.油箱中余油量Q(L)与行驶时间t(h)之间的关系如图所示。根据图象回答下列问题:
(1)小汽车行驶________h后加油, 中途加油__________L;
(2)求加油前油箱余油量Q与行驶时间t的函数关系式;
(3)如果加油站距景点200km,车速为80km/h,要到达目的地,油箱中的油是否够用?请说明理由.
如图所示,在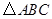 中,
中,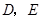 分别是
分别是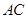 和
和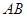 上的一点,
上的一点,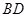 与
与 交于点
交于点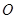 ,给出下列四个条件:①
,给出下列四个条件:①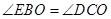 ;②
;② ;③
;③ ;④
;④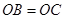 .
.
(1)上述四个条件中,哪两个条件可以判定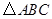 是等腰三角形(用序号写出所有的情形);
是等腰三角形(用序号写出所有的情形);
(2)选择(1)小题中的一种情形,证明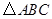 是等腰三角形.
是等腰三角形.