（年湖南湘西12分）湘西盛产椪柑，春节期间，一外地运销客户安排15辆汽车装运A、B、C三种不同品质的椪柑120吨到外地销售，按计划15辆汽车都要装满且每辆汽车只能装同一种品质的椪柑，每种椪柑所用车辆部不少于3辆．
（1）设装运A种椪柑的车辆数为x辆，装运B种椪柑车辆数为y辆，根据下表提供的信息，求出y与x之间的函数关系式；
| 椪柑品种 |
A |
B |
C |
| 每辆汽车运载量 |
10 |
8 |
6 |
| 每吨椪柑获利（元） |
800 |
1200 |
1000 |
（2）在（1）条件下，求出该函数自变量x的取值范围，车辆的安排方案共有几种？请写出每种安排方案；
（3）为了减少椪柑积压，湘西州制定出台了促进椪柑销售的优惠政策，在外地运销客户原有获利不变的情况下，政府对外地运销客户，按每吨50元的标准实行运费补贴．若要使该外地运销客户所获利润W（元）最大，应采用哪种车辆安排方案？并求出利润W（元）的最大值？
观察下列各式及验证过程：
……
⑴按照上述三个等式及验证过程中的基本思想，猜想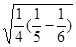
的变形结果并进行验证．
⑵针对上述各式反映的规律，写出用n（n为任意的自然数，且n≥2）表示的等式，无须证明．
已知，如图□ABCD中，AB⊥AC，AB=1，BC=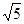
，对角线AC、BD交于0点，将直线AC绕点0顺时针旋转，分别交BC、AD于点E、F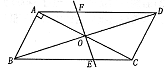
⑴求证：AF=EC；
⑵在旋转过程中，四边形BEDF可能是菱形吗?如果不能，请说明理由；如果能，说明理由并求出此时AC绕点0顺时针旋转的度数。
如图，把长方形纸片ABCD沿EF折叠，使点D与点B重合，点C落在点C′的位置上．
⑴若∠1=50°，求∠2、∠3的度数；
⑵若AB=7，DE=8，求CF的长度．
如图，在梯形ABCD中，AB∥DC， DB平分∠ADC，过点A作AE∥BD，交CD的延长线于点E，且∠C＝2∠E．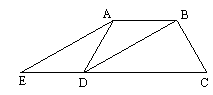
⑴求证：梯形ABCD是等腰梯形．
⑵若∠BDC＝30°，AD＝5，求CD的长．
已知如下图，正方形ABCD中，E是CD边上的一点，F为BC延长线上点，CE="CF." 
(1)求证：△BEC≌△DFC；
(2)若∠BEC=60°，求∠EFD的度数