(年四川内江12分)某汽车销售公司经销某品牌A款汽车,随着汽车的普及,其价格也在不断下降.今年5月份A款汽车的售价比去年同期每辆降价1万元,如果卖出相同数量的A款汽车,去年销售额为100万元,今年销售额只有90万元.
(1)今年5月份A款汽车每辆售价多少万元?
(2)为了增加收入,汽车销售公司决定再经销同品牌的B款汽车,已知A款汽车每辆进价为7.5万元,B款汽车每辆进价为6万元,公司预计用不多于105万元且不少于99万元的资金购进这两款汽车共15辆,有几种进货方案?
(3)如果B款汽车每辆售价为8万元,为打开B款汽车的销路,公司决定每售出一辆B款汽车,返还顾客现金a万元,要使(2)中所有的方案获利相同,a值应是多少?此时,哪种方案对公司更有利?
如图,A、B、C三点在同一直线上,分别以AB、BC为边,在直线AC的同侧作等边△ABD和等边△BCE,连接AE交BD于点M,连接CD交BE于点N,连接MN得△BMN.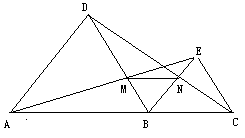
(1)求证:△ABE≌△DBC.
(2)试判断△BMN的形状,并说明理由.
如图,在等边三角形ABC中,点D,E分别在边BC,AC上,DE∥AB,过点E作EF⊥DE,交BC的延长线于点F.
(1)求∠F的度数;
(2)若CD=2,求DF的长.
在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为(-4,5),(-1,3).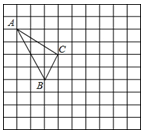
(1)请在如图所示的网格平面内作出平面直角坐标系;
(2)请作出△ABC关于y轴对称的△A′B′C′;
(3)写出点B′的坐标.
如图,已知点A、F、E、C在同一直线上,AB∥CD,∠ABE=∠CDF,AF=CE.
(1)从图中任找两组全等三角形;
(2)从(1)中任选一组进行证明.
已知(a+b)2=60,(a-b)2=80,求a2+b2及ab的值