（年浙江温州12分）八（1）班五位同学参加学校举办的数学竞赛，试卷中共有20道题，规定每题答对得5分，答错扣2分，未答得0分。赛后A，B， C，D，E五位同学对照评分标准回忆并记录了自己的答题情况（E同学只记得有7道题未答），具体如下表：
| 参赛同学 |
答对题数 |
答错题数 |
未答题数 |
| A |
19 |
0 |
1 |
| B |
17 |
2 |
1 |
| C |
15 |
2 |
3 |
| D |
17 |
1 |
2 |
| E |
/ |
/ |
7 |
（1）根据以上信息，求A，B，C，D四位同学成绩的平均分；
（2）最后获知：A，B，C，D，E五位同学成绩分别是95分，81分，64分，83分，58分.
①求E同学的答对题数和答错题数；
②经计算，A，B，C，D四位同学实际成绩平均分是80.75分，与（1）中算得的平均分不相符，发现是其中一位同学记错了自己的答题情况.请指出哪位同学记错了，并写出他的实际答题情况（直接写出答案即可）.
如图，在一面靠墙的空地上用长为24米的篱笆围成中间隔有两道篱笆的长方形花圃，设花圃的宽AB为x米，面积为y平方米．
（1）求y与x之间的函数关系式
（2）当x取何值时所围成的花圃的面积最大？最大面积是多少？
已知AB是⊙O的直径，弦CD⊥AB，垂足为P，
（1）若半径为5，CD＝8，求OP及BD的长度．
（2）若
,求
的度数．
如图，小华和小丽两人玩游戏，她们准备了A、B两个分别被平均分成三个、四个扇形的转盘．游戏规则：小华转动A盘、小丽转动B盘．转动过程中，指针保持不动，如果指针恰好指在分割线上，则重转一次，直到指针指向一个数字所在的区域为止．两个转盘停止后指针所指区域内的数字之和小于6，小华获胜．指针所指区域内的数字之和大于6，小丽获胜． 
（1）用树状图或列表法求小华、小丽获胜的概率；
（2）这个游戏规则对双方公平吗？请判断并说明理由．
如图，在平面直角坐标系中，已知点B（4，2），BA⊥x轴于A．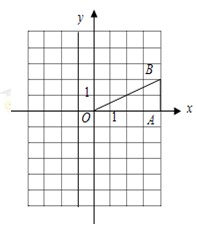
（1）画出将△OAB绕原点逆时针旋转90°后所得的△OA1B1，并写出点A1、B1的坐标；
（2）作△OAB关于原点O的中心对称图形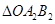
，写出对称点
、
的坐标．
将分别标有数学2，3，5的三张质地，大小完全一样的卡片背面朝上放在桌面上，
（1）随机抽取一张，求抽到奇数的概率；
（2）随机抽取一张作为个位上的数字（不放回），再抽取一张作为十位上的数字，能组成哪些两位数？并求出抽取到的两位数恰好是35的概率．