（年广东广州14分）已知平面直角坐标系中两定点A（﹣1，0）、B（4，0），抛物线y=ax2+bx﹣2（a≠0）过点A，B，顶点为C，点P（m，n）（n＜0）为抛物线上一点．
（1）求抛物线的解析式和顶点C的坐标；
（2）当∠APB为钝角时，求m的取值范围；
（3）若m＞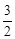
，当∠APB为直角时，将该抛物线向左或向右平移t（0＜t＜
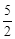）个单位，点C、P平移后对应的点分别记为C′、P′，是否存在t，使得首尾依次连接A、B、P′、C′所构成的多边形的周长最短？若存在，求t的值并说明抛物线平移的方向；若不存在，请说明理由．
已知关于x的方程
.
(1)当方程有两个不相等的实数根时,求k的取值范围;
(2)当方程的一个根是2时,求k的值.
计算：
．
如图，平面直角坐标系中，O为坐标原点，等腰梯形ABCD四个顶点都在抛物线y=ax2+bx+c上，其中点A、B在x轴上，点D在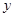
轴上，且CD∥AB, 已知S梯形ABCD=8，tan∠DAO=4，点B的坐标为（2，0），点E坐标为（0，－1）.
（1）求此抛物线的解析式；
（2）若△OEB从点B开始以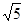
个单位每秒的速度沿BD向终点D匀速运动. 设运动时间为t秒，在整个运动过程中，当边OE与线段AD相交时，求运动时间t的取值范围；
（3）能否将△OEB绕平面内某点旋转90°后使得△OEB的两个顶点落在x轴上方的抛物线上，若能，请直接写出旋转中心的坐标，若不能，请说明理由.
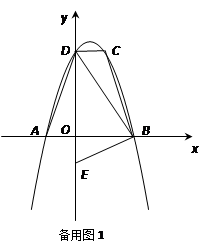
如图，边长为4的等边△AOB的顶点O在坐标原点，点A在x轴正半轴上，点B在第一象限.一动点P沿x轴以每秒1个单位长度的速度由点O向点A匀速运动，当点P到达点A时停止运动，设点P运动的时间是t秒.在点P的运动过程中，线段BP的中点为点E，将线段PE绕点P按顺时针方向旋转60º得PC.
（1）当点P运动到线段OA的中点时, 点C的坐标为 ；
（2）在点P从点O到点A的运动过程中,用含t的代数式表示点C的坐标；
（3）在点P从点O到点A的运动过程中，求出点C所经过的路径长.
在日常生活中，我们经常有目的地收集数据，分析数据，作出预测．
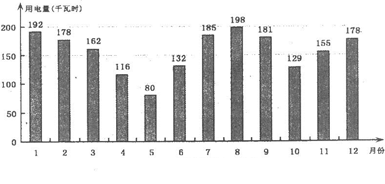
（1）下图是小芳家2011年全年月用电量的条形统计图. 根据图中提供的信息，回答下列问题：
①2011年小芳家月用电量最小的是月，四个季度中用电量最大的是第季度；
②求2011年5月至6月用电量的月增长率；
（2）今年小芳家添置了新电器．已知今年5月份的用电量是120千瓦时，根据2011年5月至7月用电量的增长趋势，预计今年7月份的用电量将达到240千瓦时．假设今年5月至6月用电量月增长率是6月至7月用电量月增长率的1.5倍，预计小芳家今年6月份的用电
量是多少千瓦时?