（年甘肃天水12分）如图（1），在平面直角坐标系中，点A（0，﹣6），点B（6，0）．Rt△CDE中，∠CDE=90°，CD=4，DE=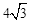
，直角边CD在y轴上，且点C与点A重合．Rt△CDE沿y轴正方向平行移动，当点C运动到点O时停止运动．解答下列问题：
（1）如图（2），当Rt△CDE运动到点D与点O重合时，设CE交AB于点M，求∠BME的度数．
（2）如图（3），在Rt△CDE的运动过程中，当CE经过点B时，求BC的长．
（3）在Rt△CDE的运动过程中，设AC=h，△OAB与△CDE的重叠部分的面积为S，请写出S与h之间的函数关系式，并求出面积S的最大值．
已知：如图，点D是∠BAC内的一点，连接BD、DC，∠A=30°，∠B+∠C=70°求∠BDC的度数.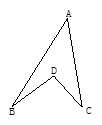
已知：如图AB∥EF。说明：∠BCF=∠B+∠F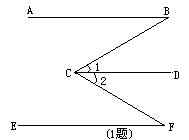
解：经过C画CD∥AB
∴∠B=∠1 （）
∵AB∥EF
而CD∥AB（画图）
∴CD∥EF （）
∴∠F=_______（）
∴∠1+∠2=∠B+∠F（）
即∠BCF=∠B+∠F
求不等式组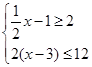
的整数解.
已知两直线l1，l2分别经过点A（1，0），点B（﹣3，0），并且当两直线同时相交于y轴正半轴的点C时，恰好有l1⊥l2，经过点A、B、C的抛物线的对称轴与直线l1交于点K，如图所示．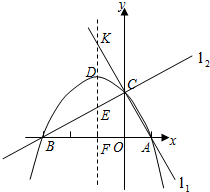
（1）求点C的坐标，并求出抛物线的函数解析式；
（2）抛物线的对称轴被直线l1，抛物线，直线l2和x轴依次截得三条线段，问这三条线段有何数量关系？请说明理由；
（3）当直线l2绕点C旋转时，与抛物线的另一个交点为M，请找出使△MCK为等腰三角形的点M，简述理由，并写出点M的坐标．
某中学课外活动小组准备围建一个矩形生物苗圃园，其中一边靠墙，另外三边用长为50米的篱笆围成。已知墙长为26米（如图所示），设这个苗圃园平行于墙的一边的长为
米。（1）若垂直于墙的一边长为
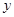米，直接写出与的函数关系式及其自变量的取值范围；（2）当为多少米时，这个苗圃园的面积最大，并求出这个最大值；（3）当这个苗圃园的面积不小于300平方米时，试结合函数图象，求出的取值范围。