某中学课外活动小组准备围建一个矩形生物苗圃园,其中一边靠墙,另外三边用长为50米的篱笆围成。已知墙长为26米(如图所示),设这个苗圃园平行于墙的一边的长为 米。(1)若垂直于墙的一边长为
米。(1)若垂直于墙的一边长为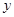 米,直接写出
米,直接写出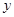 与
与 的函数关系式及其自变量
的函数关系式及其自变量 的取值范围;(2)当
的取值范围;(2)当 为多少米时,这个苗圃园的面积最大,并求出这个最大值;(3)当这个苗圃园的面积不小于300平方米时,试结合函数图象,求出
为多少米时,这个苗圃园的面积最大,并求出这个最大值;(3)当这个苗圃园的面积不小于300平方米时,试结合函数图象,求出 的取值范围。
的取值范围。
(1)用小立方块搭成的几何体,主视图和俯视图如下图,问搭成这样的几何体最多要小立方块,最少要小立方块.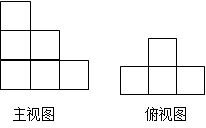
(2)世园会期间,西安某学校组织教师和学生参观世园会,每位教师的车费为m元,每位学生的车费为n元,学生每满100人可优惠2人的车费,如果该校七年级有教师20人,学生612人,则需要付给汽车公司的总费用为_______元.
西安市绿色出租汽车收费标准为:起步价(不超过3千米)为6元,3千米后每千米加收1.5元.小明人乘坐这种出租车行驶了x千米 (x≥3).
(1)先试用代数式表示他应付的车费;
(2)当x = 4千米时,他应付车费多少元?
出租车司机小李某天下午运营全是在东西走向的东西大街上进行的,如果规定向东为正,向西为负,这天下午他的行车里程(单位:千米)如下:
+15,-3,+5,-3,+10,-3,-4,+12,+4,-5,+6
(1)将最后一名乘客送到目的地时,小李距下午出车时的出发点多远?
(2)若汽车耗油量为0.07升/千米,这天下午小李共耗油多少升?
(1)3a-2b-5a-b
(2)化简求值:2(x-y)-(-x-4y ),其中 ,y=1
,y=1
计算题:
(1)1 (2)
(2)