(年湖南湘西22分)如图,抛物线y=ax2+bx+c关于y轴对称,它的顶点在坐标原点O,点B(2,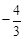 )和点C(﹣3,﹣3)两点均在抛物线上,点F(0,
)和点C(﹣3,﹣3)两点均在抛物线上,点F(0,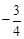 )在y轴上,过点(0,
)在y轴上,过点(0,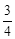 )作直线l与x轴平行.
)作直线l与x轴平行.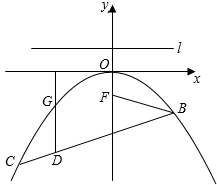
(1)求抛物线的解析式和直线BC的解析式.
(2)设点D(x,y)是线段BC上的一个动点(点D不与B,C重合),过点D作x轴的垂线,与抛物线交于点G.设线段GD的长度为h,求h与x之间的函数关系式,并求出当x为何值时,线段GD的长度h最大,最大长度h的值是多少?
(3)若点P(m,n)是抛物线上位于第三象限的一个动点,连接PF并延长,交抛物线于另一点Q,过点Q作QS⊥l,垂足为点S,过点P作PN⊥l,垂足为点N,试判断△FNS的形状,并说明理由;
(4)若点A(﹣2,t)在线段BC上,点M为抛物线上的一个动点,连接AF,当点M在何位置时,MF+MA的值最小,请直接写出此时点M的坐标与MF+MA的最小值.
如图是由6个相同的正方形拼成的图形,请你将其中一个正方形移动到合适的位置,使它与另5个正方形能拼成一个正方体的表面展开图.(请在图中将要移动的那个正方形涂黑,并画出移动后的正方形).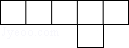
2015秋•永登县期末)为响应国家要求中小学生每天锻练1小时的号召,某校开展了形式多样的“阳光体育运动”活动,小明对某班同学参加锻炼的情况进行了统计,并绘制了下面的图1和图2.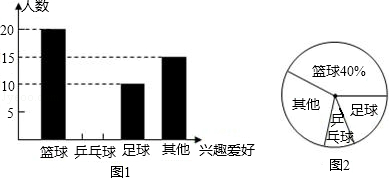
(1)求被调查的班级的学生人数;
(2)求喜欢“乒乓球”的学生人数,并在图1中将“乒乓球”部分的图形补充完整;
(3)若该校共有2000名学生,请估计喜欢“足球”的学生人数.
解方程:
(1)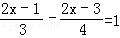
(2)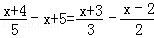 .
.
当 时,求代数式3(x2﹣2xy)﹣[3x2﹣2y+2(xy+y)]的值.
时,求代数式3(x2﹣2xy)﹣[3x2﹣2y+2(xy+y)]的值.
某景区门票价格80元/人,景区为吸引游客,对门票价格进行动态管理,非节假日打6折,节假日期间,10人以下(包括10人)不打折,10人以上超过10人的部分打8折,导游小王6月10日(非节假日)带A旅游团,6月20日(端午节)带B旅游团到该景区旅游,两团共计50人,两次共付门票费用3040元,求A、B两个旅游团各多少人?