(年湖南岳阳10分)如图,抛物线经过点A(1,0),B(5,0),C(0, )三点,设点E(x,y)是抛物线上一动点,且在x轴下方,四边形OEBF是以OB为对角线的平行四边形.
)三点,设点E(x,y)是抛物线上一动点,且在x轴下方,四边形OEBF是以OB为对角线的平行四边形.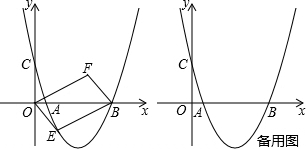
(1)求抛物线的解析式;
(2)当点E(x,y)运动时,试求平行四边形OEBF的面积S与x之间的函数关系式,并求出面积S的最大值?
(3)是否存在这样的点E,使平行四边形OEBF为正方形?若存在,求E点,F点的坐标;若不存在,请说明理由.
如图,小岛A在港口P的南偏西45°方向,距离港口81海里处.甲船从A出发,沿AP方向以9海里/时的速度驶向港口,乙船从港口P出发,沿南偏东60°方向,以18海里/时的速度驶离港口,现两船同时出发.
出发后几小时两船与港口P的距离相等?
出发后几小时乙船在甲船的正东方向?(结果精确到0.1小时)
(参考数据: ≈1.41,
≈1.41, ≈1.73)
≈1.73)
如图,甲转盘被分成3个面积相等的扇形,乙转盘被分成4个面积相等的扇形,每一个扇形都标有相应的数字.同时转动两个转盘,当转盘停止后,设甲转盘中指针所指区域内的数字为x,乙转盘中指针所指区域内的数字为y(当指针指在边界上时,重转一次,直到指针指向一个区域为止).
请你用画树状图或列表格的方法,求出点(x, y)落在第二象限内的概率;
求出点(x, y)落在函数y=-
 图象上的概率.
图象上的概率.
如图,矩形ABCD中,O是AC与BD的交点,过O点的直线EF与AB, CD的延长线分别交于E,F.
求证:△BOE≌△DOF;
在现有条件下,再添加EF与AC满足什么关系时,以A,E,C,F为顶点的四边形是菱形?
如图,D是反比例函数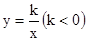 的图像上一点,过D作DE⊥x轴于E, DC⊥y轴于C,一次函数y=-x+m与y=-
的图像上一点,过D作DE⊥x轴于E, DC⊥y轴于C,一次函数y=-x+m与y=-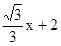 的图象都经过点C,与x轴分别交于A、B两点,四边形DCAE的面积为4,求k的值.
的图象都经过点C,与x轴分别交于A、B两点,四边形DCAE的面积为4,求k的值.
某区有3000名学生参加知识竞赛.为了了解本次知识竞赛的成绩分布情况,从中抽取了200名学生的得分(得分取正整数,满分为100分)进行统计.
| 分组 |
频数 |
频率 |
| 49.5~59.5 |
10 |
|
| 59.5~69.5 |
16 |
0.08 |
| 69.5~79.5 |
0.20 |
|
| 79.5~89.5 |
62 |
|
| 89.5~100.5 |
72 |
0.36 |
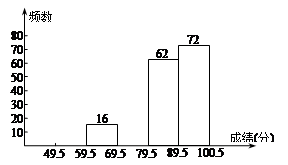
请你根据不完整的频率分布表,解答下列问题:补全频数分布直方图
若将得分转化为等级,规定得分低于59.5分评为“D”,59.5~69.5分评为“C”,69.5~89.5分评为“B”,89.5~100.5分评为“A”.这次全区参加竞赛的学生中约有多少成绩被评为“D”?如果随机抽查一名参赛学生的成绩等级,则这名学生的成绩被评为“A”、“B”、“C”、“D”哪一个等级的可能性大?请说明理由.