(本小题12分) 菱形ABCD的边长为2,∠BAD=60°,对角线AC,BD相交于点O,动点P在线段AC上从点A向点C运动,过P作PE∥AD,交AB于点E,过P作PF∥AB,交AD于点F,四边形QHCK与四边形PEAF关于直线BD对称. 设菱形ABCD被这两个四边形盖住部分的面积为S1,AP=x:
(1)对角线AC的长为 ;S菱形ABCD= ;
(2)用含x的代数式表示S1;
(3)设点P在移动过程中所得两个四边形PEAF与QHCK的重叠部分面积为S2,当S2= S菱形ABCD时,求x的值.
S菱形ABCD时,求x的值.
结合数轴与绝对值的知识回答下列问题:
(1)数轴上表示4和1的两点之间的距离是;表示-3和2两点之间的距离是;一般地,数轴上表示数m和数n的两点之间的距离等于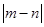 .如果表示数
.如果表示数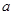 和-2的两点之间的距离是3,那么
和-2的两点之间的距离是3,那么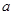 =;
=;
(2)若数轴上表示数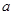 的点位于-4与2之间,求
的点位于-4与2之间,求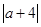 +
+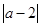 的值;
的值;
有长为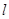 的篱笆,利用它和房屋的一面墙围成如图形状的园子,园子的宽为
的篱笆,利用它和房屋的一面墙围成如图形状的园子,园子的宽为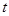 .
.
(1)利用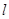 ,
,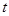 的代数式表示园子的面积;
的代数式表示园子的面积;
(2)当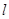 =80米,
=80米,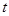 =15米时,求园子的面积。
=15米时,求园子的面积。
把数轴画完整,并在在数轴上表示下列各数,然后按从小到大的顺序用“<”号连接.
-3, 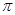 , 2,
, 2, 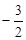 .
.
解方程:① 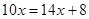 ②
②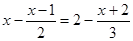
先化简,再求值.
(1)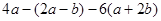 其中
其中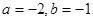 .
.
(2)已知x+3y="3" ,xy=11,求代数式3(x-3y)-(xy+5)+2(3y-2x)的值.