先化简，再求值．
(1)
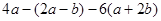其中
．
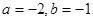（2）已知x+3y="3" ，xy=11，求代数式3（x-3y）-(xy+5)+2(3y-2x)的值.
如图,抛物线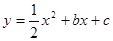
（b,c是常数,且c＜0）与
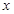轴分别交于点A、B（点A位于点B的左侧）,与
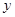轴的负半轴交于点C,点A的坐标为(－1,0)．
（1）请直接写出点OA的长度;
（2）若常数b,c满足关系式：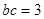
．求抛物线的解析式．
（3）在（2）的条件下,点P是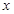轴下方抛物线上的动点,连接PB、PC．设△PBC的面积为S．
①求S的取值范围;
②若△PBC的面积S为整数,则这样的△PBC共有多少个（直接写出结果）？
四边形ABCD中,点E是AB的中点,F是AD边上的动点．连结DE、CF．
（1）若四边形ABCD是矩形,AD=12,CD=10,如图（1）所示．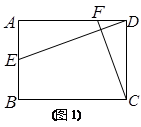
①请直接写出AE的长度;
②当DE⊥CF时,试求出CF长度．
（2）如图（2）,若四边形ABCD是平行四边形,DE与CF相交于点P．
探究：当∠B与∠PC满足什么关系时,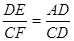
成立？并证明你的结论．
小明利用暑假20天（8月5日至24日）参与了一家网店经营的社会实践．负责在网络上销售一种新款的SD卡,每张成本价为20元．第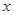
天销售的相关信息如下表所示．
| 销售量p（张） |
 |
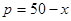| 销售单价q（元/张） |
 |
（1）请计算哪一天SD卡的销售单价为35元？
（2）在这20天中,在网络上这款销售SD卡在哪一天获得利润最大？这一天赚了多少元？
为培养学生的创造性思维,学校举行科技小制作比赛．对公开征集到的科技小制作作品的数量进行了分析统计,并制作了如下统计图．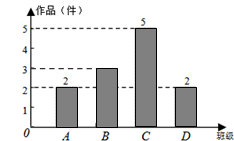
（1）学校共征集到作品共 件;
（2）经过评选后,有2名男生和2名女生获得一等奖．现要从这4位同学中抽两人去参加表彰座谈会,请用树状图或列表法求出恰好抽中一男一女的概率．
如图,防洪大堤的横断面是梯形ABCD,其中AD//BC,坡长AB=10cm,坡角
,汛期来临前对其进行了加固,改造后的背水面坡角
．(注：请在结果中保留根号)
（1）试求出防洪大堤的横断面的高度;
（2）请求出改造后的坡长AE．