四边形ABCD中,点E是AB的中点,F是AD边上的动点.连结DE、CF.
(1)若四边形ABCD是矩形,AD=12,CD=10,如图(1)所示.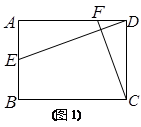
①请直接写出AE的长度;
②当DE⊥CF时,试求出CF长度.
(2)如图(2),若四边形ABCD是平行四边形,DE与CF相交于点P.
探究:当∠B与∠PC满足什么关系时,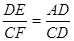 成立?并证明你的结论.
成立?并证明你的结论.
函数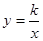 和
和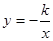
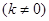 的图象关于
的图象关于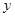 轴对称,我们把函数
轴对称,我们把函数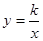 和
和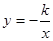
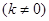 叫做互为“镜子”函数.类似地,如果函数
叫做互为“镜子”函数.类似地,如果函数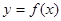 和
和 的图象关于
的图象关于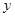 轴对称,那么我们就把函数
轴对称,那么我们就把函数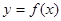 和
和 叫做互为“镜子”函数.
叫做互为“镜子”函数.
(1)请写出函数y=2x-3的“镜子”函数: ▲;
(2)函数 ▲的“镜子”函数是y=-x2+2x+3;
(3)如图,一条直线与一对“镜子”函数 (
(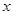 >
> )和
)和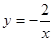 (
(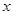 <
< )的图象分别交于点A,B,C,如果
)的图象分别交于点A,B,C,如果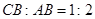 ,点
,点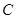 在函数
在函数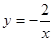 (
(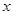 <
< )的“镜子”函数上的对应点的横坐标是1/2,求点
)的“镜子”函数上的对应点的横坐标是1/2,求点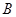 的坐标.
的坐标.
2012年4月11日,印尼北苏门答腊西岸发生里氏8.6级特大地震,造成重大人员伤亡和财产损失.强震发生后,中国军队将筹措到位的第一批援印尼救灾物资打包成件,其中棉帐篷和毛巾被共3200件,毛巾被比棉帐篷多800件.
(1)求打包成件的棉帐篷和毛巾被各多少件?
(2)现计划用甲、乙两种小飞机共8架,一次性将这批棉帐篷和毛巾被全部运往印尼重灾区.已知甲种飞机最多可装毛巾被400件和棉帐篷100件,乙种飞机最多可装毛巾被和棉帐篷各200件.则安排甲、乙两种飞机时有几种方案?请你帮助设计出来.
(3)在第(2)问的条件下,如果甲种飞机每架需运输成本费4000元,乙种飞机每架需付运输成本费3600元.应选择哪种方案可使运输成本费最少?最少运输成本费是多少元?
已知:如图,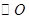 半径
半径 垂直于弦
垂直于弦 ,点
,点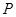 在
在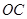 的延长线上,
的延长线上, 平分
平分 .
.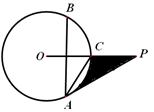
(1) 求证: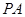 是
是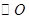 的切线
的切线
(2) 如果 =
=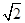 ,
,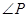 =30°,求阴影部分面积.(保留根号和
=30°,求阴影部分面积.(保留根号和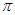 )
)
“体验·创新·成长”这是2012某市第八届少年科技大赛的宗旨.比赛分为四类:优秀科技实践活动、科技创新活动项目、优秀少儿科学幻想绘画、科技创新成果.评委对所有的参赛作品进行了分类统计,各类参赛作品按一定的百分比设奖,并对获奖作品也进行分类,制作了如下的条形统计图及扇形统计图:
作根据上述信息,完成下列问题:
(1) 参赛获奖品总数是件;
(2) 算出获奖优秀科技实践活动所在扇形的圆心角的度数,并将条形图补充完整;
(3)全市中小学生参加少年科技大赛热情高涨,在2012参赛作品328件的基础上逐年增长,预计2014年参赛作品将有738件,求平均每年的增长率是多少?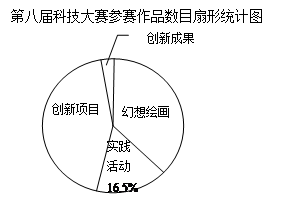

如图,在矩形ABCD中,O是AC与BD的交点,过O点的直线EF与AB、CD的延长线分别交于E、F.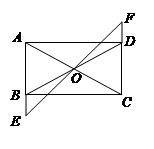
(1)求证:△BOE≌△DOF;
(2)当EF与AC满足____▲_____关系时,以A、E、C、F为顶点的四边形是菱形.