（年四川攀枝花12分）如图，抛物线
（a＞0）与x轴交于A、B两点（A在B的左侧），与y轴交于点C，点D的坐标为（﹣6，0），且∠ACD=90°．
（1）请直接写出A、B两点的坐标；
（2）求抛物线的解析式；
（3）抛物线的对称轴上是否存在点P，使得△PAC的周长最小？若存在，求出点P的坐标及周长的最小值；若不存在，说明理由；
（4）平行于y轴的直线m从点D出发沿x轴向右平行移动，到点A停止．设直线m与折线DCA的交点为G，与x轴的交点为H（t，0）．记△ACD在直线m左侧部分的面积为s，求s关于t的函数关系式及自变量t的取值范围．
（本小题满分5分）已知直线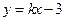
经过点M（2，1），且与x轴交于点A，与y轴交于点B．
（1）求k的值；
（2）求A、B两点的坐标；
（3）过点M作直线MP与y轴交于点P，且△MPB的面积为2，求点P的坐标．
（本小题满分5分）列方程或方程组解应用题：
某学校组织九年级学生参加社会实践活动，若单独租用35座客车若干辆，则刚好坐满；若单独租用55座客车，则可以少租一辆，且余45个空座位，求该校九年级学生参加社会实践活动的人数．
（本小题满分5分）已知
，求代数式
的值．
（本小题满分5分）如图，A、B、C三点在同一条直线上，AB=2BC，分别以AB，BC为边做正方形ABEF和正方形BCMN，联结FN，EC． 求证：FN=EC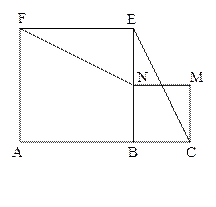
（本小题满分5分）解方程： 
．