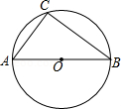
(年贵州黔西南16分)如图所示,在平面直角坐标系中,抛物线y=ax2+bx+c经过A(﹣3,0)、B(1,0)、C(0,3)三点,其顶点为D,连接AD,点P是线段AD上一个动点(不与A、D重合),过点P作y轴的垂线,垂足点为E,连接AE.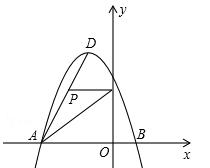
(1)求抛物线的函数解析式,并写出顶点D的坐标;
(2)如果P点的坐标为(x,y),△PAE的面积为S,求S与x之间的函数关系式,直接写出自变量x的取值范围,并求出S的最大值;
(3)在(2)的条件下,当S取到最大值时,过点P作x轴的垂线,垂足为F,连接EF,把△PEF沿直线EF折叠,点P的对应点为点P′,求出P′的坐标,并判断P′是否在该抛物线上.
甲队修路500米与乙队修路800米所用天数相同,乙队比甲队每天多修30米,问甲队每天修路多少米?
解:设甲队每天修路 米,用含 的代数式完成表格:
|
甲队每天修路长度(单位:米) |
乙队每天修路长度(单位:米) |
甲队修500米所用天数(单位:天) |
乙队修800米所用天数(单位:天) |
|
|
|
|
|
关系式:甲队修500米所用天数 乙队修800米所用天数
根据关系式列方程为:
解得:
检验:
答: .
为确保信息安全,在传输时往往需加密,发送方发出一组密码 , , 时,则接收方对应收到的密码为 , , .双方约定: , , ,例如发出1,2,3,则收到0,4,5
(1)当发送方发出一组密码为2,3,5时,则接收方收到的密码是多少?
(2)当接收方收到一组密码2,8,11时,则发送方发出的密码是多少?
如图,直线 交 轴于点 ,交 轴于点 ,过 , 两点的二次函数 的图象交 轴于另一点 .
(1)求二次函数的表达式;
(2)连接 ,点 是线段 上的动点,作 轴交二次函数的图象于点 ,求线段 长度的最大值;
(3)若点 为二次函数 图象的顶点,点 是该二次函数图象上一点,在 轴、 轴上分别找点 , ,使四边形 的周长最小,求出点 , 的坐标.
温馨提示:在直角坐标系中,若点 , 的坐标分别为 , , , ,
当 平行 轴时,线段 的长度可由公式 求出;
当 平行 轴时,线段 的长度可由公式 求出.
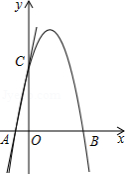
(1)阅读理解:
如图①,在 中,若 , ,求 边上的中线 的取值范围.
解决此问题可以用如下方法:延长 到点 使 ,再连接 (或将 绕着点 逆时针旋转 得到 ,把 、 , 集中在 中,利用三角形三边的关系即可判断.
中线 的取值范围是 ;
(2)问题解决:
如图②,在 中, 是 边上的中点, 于点 , 交 于点 , 交 于点 ,连接 ,求证: ;
(3)问题拓展:
如图③,在四边形 中, , , ,以 为顶点作一个 角,角的两边分别交 , 于 、 两点,连接 ,探索线段 , , 之间的数量关系,并加以证明.
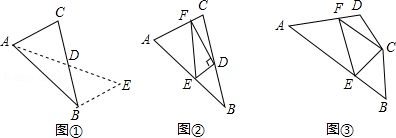
如图, 是 的外接圆, 是 的直径, .
(1)利用尺规,作 的平分线,交 于点 ;(保留作图痕迹,不写作法)
(2)在(1)的条件下,连接 , ,若 ,求 的度数;
(3)在(2)的条件下, 交 于点 ,求由线段 , , 所围成区域的面积.(其中 表示劣弧,结果保留 和根号)