(年湖南岳阳10分)如图,抛物线经过点A(1,0),B(5,0),C(0,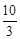 )三点,设点E(x,y)是抛物线上一动点,且在x轴下方,四边形OEBF是以OB为对角线的平行四边形.
)三点,设点E(x,y)是抛物线上一动点,且在x轴下方,四边形OEBF是以OB为对角线的平行四边形.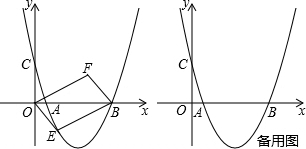
(1)求抛物线的解析式;
(2)当点E(x,y)运动时,试求平行四边形OEBF的面积S与x之间的函数关系式,并求出面积S的最大值?
(3)是否存在这样的点E,使平行四边形OEBF为正方形?若存在,求E点,F点的坐标;若不存在,请说明理由.
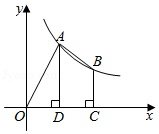
如图,在平面直角坐标系中, 为坐标原点,点 , 在函数 的图象上(点 的横坐标大于点 的横坐标),点 的坐标为 ,过点 作 轴于点 ,过点 作 轴于点 ,连接 , .
(1)求 的值.
(2)若 为 中点,求四边形 的面积.
如图,某班数学小组测量塔的高度,在与塔底部 相距 的 处,用高 的测角仪 测得该塔顶端 的仰角 为 .求塔 的高度(结果精确到 .
(参考数据: , ,

图①、图②、图③都是 的正方形网格,每个小正方形的顶点称为格点. , , 均为格点.在给定的网格中,按下列要求画图:

(1)在图①中,画一条不与 重合的线段 ,使 与 关于某条直线对称,且 , 为格点.
(2)在图②中,画一条不与 重合的线段 ,使 与 关于某条直线对称,且 , 为格点.
(3)在图③中,画一个 ,使 与 关于某条直线对称,且 , , 为格点.
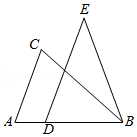
如图,在 中, ,点 在边 上,且 ,过点 作 ,并截取 ,且点 , 在 同侧,连接 .求证: .
甲、乙二人做某种机械零件.已知甲每小时比乙多做6个,甲做90个所用的时间与乙做60个所用的时间相等.求乙每小时做零件的个数.