（年江苏连云港14分）某数学兴趣小组对线段上的动点问题进行探究，已知AB=8．
问题思考：
如图1，点P为线段AB上的一个动点，分别以AP、BP为边在同侧作正方形APDC与正方形PBFE．
（1）在点P运动时，这两个正方形面积之和是定值吗？如果时求出；若不是，求出这两个正方形面积之和的最小值．
（2）分别连接AD、DF、AF，AF交DP于点A，当点P运动时，在△APK、△ADK、△DFK中，是否存在两个面积始终相等的三角形？请说明理由．
问题拓展：
（3）如图2，以AB为边作正方形ABCD，动点P、Q在正方形ABCD的边上运动，且PQ=8．若点P从点A出发，沿A→B→C→D的线路，向D点运动，求点P从A到D的运动过程中，PQ的中点O所经过的路径的长．
（4）如图（3），在“问题思考”中，若点M、N是线段AB上的两点，且AM=BM=1，点G、H分别是边CD、EF的中点．请直接写出点P从M到N的运动过程中，GH的中点O所经过的路径的长及OM+OB的最小值．
已知关于x的一元二次方程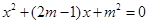
有两个实数根
、
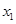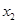，并且满足
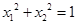，求m的值．
解方程（每小题4分，共16分）
（1）
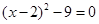
（2）
（3）
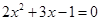
（4）
己知：二次函数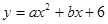
与x轴交于A、B两点（点A在点B的左侧），点A、点B的横坐标分别为一元二次方程
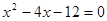的两个根．
（1）求出该二次函数表达式及顶点坐标；
（2）如图1，在抛物线对称轴上是否存在点P，使△APC的周长最小，若存在，请求出点P的坐标：若不存在，请说明理由；
（3）如图2，连接AC、BC，点Q是线段OB上一个动点（点Q不与点O、B重合）．过点Q作QD∥AC交BC于点D，设Q点坐标（m，0），当△CDQ面积S最大时，求m的值．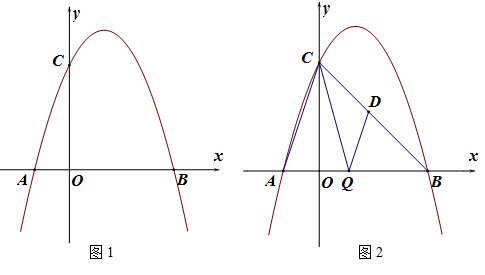 
已知：关于x的函数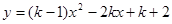
的图象与x轴有交点．
（1）求k的取值范围；
（2）若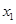
，
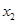是函数图象与x轴两个交点的横坐标，且满足
．
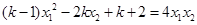①求k的值；②当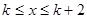
时，求函数y的最大值和最小值．
小丽为校合唱队购买某种服装时，商店经理给出了如下优惠条件：如果一次性购买不超过10件，单价为80元：如果一次性购买多于10件，那么每增加1件，购买的所有服装的单价降低2元，但单价不得低于50元．按此优惠条件，小丽一次性购买了这种服装x件．
（1）当x= 时，小丽购买的这种服装的单价为76元；
（2）小丽一次性购买这种服装付了1200元．请问她购买了多少件这种服装？