（年山西省13分）综合与探究：如图，在平面直角坐标系xOy中，四边形OABC是平行四边形，A、C两点的坐标分别为（4，0），（﹣2，3），抛物线W经过O、A、C三点，D是抛物线W的顶点．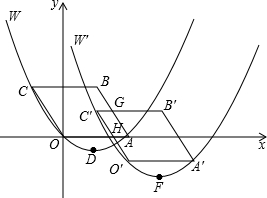
（1）求抛物线W的解析式及顶点D的坐标；
（2）将抛物线W和
OABC一起先向右平移4个单位后，再向下平移m（0＜m＜3）个单位，得到抛物线W′和O′A′B′C′，在向下平移的过程中，设O′A′B′C′与OABC的重叠部分的面积为S，试探究：当m为何值时S有最大值，并求出S的最大值；
（3）在（2）的条件下，当S取最大值时，设此时抛物线W′的顶点为F，若点M是x轴上的动点，点N时抛物线W′上的动点，试判断是否存在这样的点M和点N，使得以D、F、M、N为顶点的四边形是平行四边形？若存在，请直接写出点M的坐标；若不存在，请说明理由．
