如图是一个几何体的主视图与俯视图,求该几何体的体积.(π取3.14)
如图,AB为⊙O的直径,点C在⊙O上,延长BC至点D,使DC=CB,延长DA
与⊙O的另一个交点为E,连结AC,CE。
(1)求证:∠B=∠D;
(2)若AB=4,BC-AC=2,求CE的长。
一个不透明的袋中装有5个黄球、13个黑球和22个红球,它们除颜色外都相同。
(1)求从袋中摸出一个球是黄球的概率;
(2)现从袋中取出若干个黑球,并放入相同数量的黄球,搅拌均匀后,使从袋中摸出一个球是黄球的概率不小于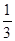 ,问至少取出了多少个黑球?
,问至少取出了多少个黑球?
如图,抛物线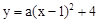 与x轴交于点A,B,与
与x轴交于点A,B,与 轴交于点C。过点C作CD∥x轴,交抛物线的对称轴于点D,连结BD。已知点A坐标为(-1,0)。
轴交于点C。过点C作CD∥x轴,交抛物线的对称轴于点D,连结BD。已知点A坐标为(-1,0)。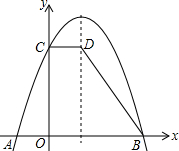
(1)求该抛物线的解析式;
(2)求梯形COBD的面积。
如果三角形有一边上的中线长恰好等于这边的长,那么称这个三角形为“好玩三角形”
(1)请用直尺与圆规画一个“好玩三角形”;
(2)如图1,在Rt△ABC中,∠C=90°,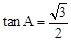 ,求证:△ABC是“好玩三角形”;
,求证:△ABC是“好玩三角形”;
(3)如图2,已知菱形ABCD的边长为a, ∠ABC=2β,点P,Q从点A同时出发,以相同的速度分别沿折线AB-BC和AD-DC向终点C运动,记点P所经过的路程为s
①当β=45°时,若△APQ是“好玩三角形”,试求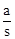 的值;
的值;
②当tanβ的取值在什么范围内,点P,Q在运动过程中,有且只有一个△APQ能成为“好玩三角形”?请直接写出tanβ的取值范围。
(4)本小题为选做题
依据(3)中的条件,提出一个关于“在点P,Q的运动过程中,tanβ的取值范围与△APQ是“好玩三角形”的个数关系”的真命题(“好玩三角形”的个数限定不能为1)。
如图1,已知直线 与y轴交于点A,抛物线
与y轴交于点A,抛物线 经过点A,其顶点为B,另一抛物线
经过点A,其顶点为B,另一抛物线 的顶点为D,两抛物线相交于点C
的顶点为D,两抛物线相交于点C
(1)求点B的坐标,并说明点D在直线 的理由;
的理由;
(2)设交点C的横坐标为m
①交点C的纵坐标可以表示为:或,由此请进一步探究m关于h的函数关系式;
②如图2,若 ,求m的值
,求m的值