(年山东莱芜12分)如图,过A(1,0)、B(3,0)作x轴的垂线,分别交直线y=4﹣x于C、D两点.抛物线y=ax2+bx+c经过O、C、D三点.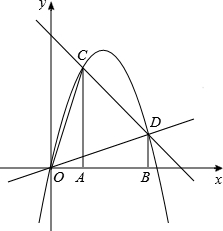
(1)求抛物线的表达式;
(2)点M为直线OD上的一个动点,过M作x轴的垂线交抛物线于点N,问是否存在这样的点M,使得以A、C、M、N为顶点的四边形为平行四边形?若存在,求此时点M的横坐标;若不存在,请说明理由;
(3)若△AOC沿CD方向平移(点C在线段CD上,且不与点D重合),在平移的过程中△AOC与△OBD重叠部分的面积记为S,试求S的最大值.
(本题6分)如图:直线DE交△ABC的边AB、AC于D、E,交BC延长线于F,若∠B=67°,∠ACB=74°,
∠AED=48°,求∠BDF的度数。
如图,平面直角坐标系中,点B的坐标为(1,2),过点B作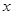 轴的垂线,垂足为A,连结OB,将△OAB沿OB折叠,使点A落在点A′处,A′B与
轴的垂线,垂足为A,连结OB,将△OAB沿OB折叠,使点A落在点A′处,A′B与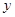 轴交于点F.
轴交于点F.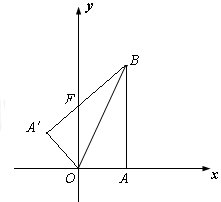
(1)求证:OF=BF;
(2)求BF的长;
(3)求过点A′的双曲线的解析式。
如图,一次函数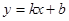 的图像与反比例函数
的图像与反比例函数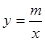 的图像交于
的图像交于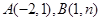 两点。
两点。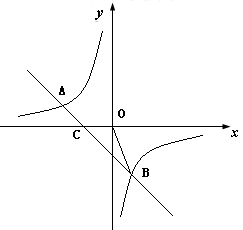
求:(1)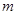 的值;
的值;
(2)求一次函数的解析式;
(3)若直线AB交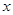 轴于点C,求△OBC的面积.
轴于点C,求△OBC的面积.
.一辆汽车开往距离出发地180千米的目的地,出发后第一小时内按原计划的速度匀速行驶,一小时后以原来速度的1.5倍匀速行驶,并比原计划提前40分到达目的地.求前一小时的行驶速度.
如图,在反比例函数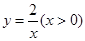 的图象上,有点
的图象上,有点 ,
,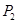 ,
, ,
,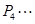 ,它们的横坐标依次为1,2,3,4
,它们的横坐标依次为1,2,3,4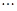 .分别过这些点作
.分别过这些点作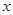 轴与
轴与 轴的垂线,图中所构成的阴影部分的面积从左到右依次为
轴的垂线,图中所构成的阴影部分的面积从左到右依次为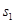 ,
,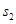 ,
,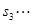
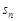 ,求:
,求:
(1) 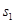 的值;
的值;
(2) 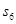 的值;
的值;
(3) 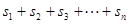 的值。(用含
的值。(用含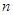 的代数式来表示)
的代数式来表示)