（年甘肃兰州12分）如图，抛物线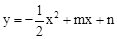
与x轴交于A、B两点，与y轴交于点C，抛物线的对称轴交x轴于点D，已知A（﹣1，0），C（0，2）．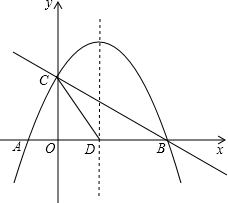
（1）求抛物线的表达式；
（2）在抛物线的对称轴上是否存在点P，使△PCD是以CD为腰的等腰三角形？如果存在，直接写出P点的坐标；如果不存在，请说明理由；
（3）点E时线段BC上的一个动点，过点E作x轴的垂线与抛物线相交于点F，当点E运动到什么位置时，四边形CDBF的面积最大？求出四边形CDBF的最大面积及此时E点的坐标．
已知一个角的补角比这个角的余角的3倍大10°，求这个角的度数．
先化简，再求值：﹣（﹣a2+2ab+b2）+（﹣a2﹣ab+b2），其中a=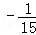
，b=10．
解下列方程
（1）
；
（2）
=3．
计算
（1）﹣14﹣2×（﹣3）2+|﹣4|
（2）（﹣
）÷
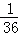
（3）2（2b﹣3a）+3（2a﹣3b）
（4）180°﹣56°23′．
如图，抛物线与x轴交于点A(－1，0)、B(3，0)，与y轴交于点C(0，3)．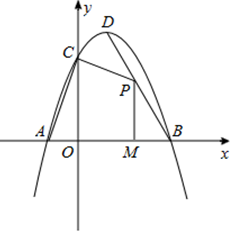
（1）求抛物线的解析式及顶点D的坐标；
（2）若点P是抛物线第一象限上的一个动点，过点P作PQ∥AC交x轴于点Q．当点P的坐标为时，四边形PQAC是平行四边形;当点P的坐标为 时，四边形PQAC是等腰梯形. (利用备用图画图，直接写出结果，不写求解过程)．
（3）若P为线段BD上的一个动点，过点P作PM⊥x轴于点M，求四边形PMAC的面积的最大值和此时点P的坐标