如图,抛物线与x轴交于点A(-1,0)、B(3,0),与y轴交于点C(0,3).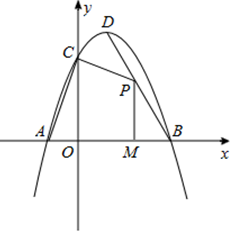
(1)求抛物线的解析式及顶点D的坐标;
(2)若点P是抛物线第一象限上的一个动点,过点P作PQ∥AC交x轴于点Q.当点P的坐标为 时,四边形PQAC是平行四边形;当点P的坐标为 时,四边形PQAC是等腰梯形. (利用备用图画图,直接写出结果,不写求解过程).
(3)若P为线段BD上的一个动点,过点P作PM⊥x轴于点M,求四边形PMAC的面积的最大值和此时点P的坐标
解方程: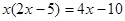
小明选购手机卡,了解到有两种计费方式:
联通如意通:月租费30元,本地通话费0.10元/分;
移动神州行:无月租费,本地通话费0.30元/分。
(1)小明估计他每月的本地通话大约为120分钟,请问他应选择哪种手机卡较优惠?
(2)小明愿意每月拿出60元支付手机费用,若要每月用完这60元,则应选择哪种手机卡较合算?
(3)每月本地通话时间为多少分钟两种手机卡费用相同?费用是多少?并根据你的计算结果,回答在什么情况下,使用联通如意通合算?在什么情况下,使用移动神州行合算?
一架飞机在两城之间飞行,风速为24千米 /小时 ,顺风飞行需2小时50分,逆风飞行需要3小时。求无风时飞机的飞行速度和两城之间的航程。
某车间有工人85人,平均每人每天可加工大齿轮12个或小齿轮10个,又知一个大齿轮与两个小齿轮配成一套,问应如何安排工人才能使每天生产的产品刚好成套?
如图,点A、O、E在同一直线上,∠AOB=40°,∠DOE=28°,OD平分∠COE, 求∠BOC的度数。