（年重庆市B12分）如图1，在□ABCD中，AH⊥DC，垂足为H，AB＝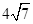
，AD＝7，AH＝
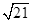.现有两个动点E、F同时从点A出发，分别以每秒1个单位长度、每秒3个单位长度的速度沿射线AC方向匀速运动. 在点E、F运动过程中，以EF为边作等边△EFG，使△EFG与△ABC在射线AC的同侧，当点E运动到点C时，E、F两点同时停止运动. 设运转时间为t秒.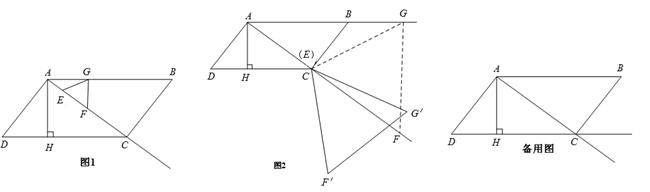
（1）求线段AC的长；
（2）在整个运动过程中，设等边△EFG与△ABC重叠部分的面积为S，请直接写出S与t之间的函数关系式，并写出相应的自变量t的取值范围；
（3）当等边△EFG的顶点E到达点C时，如图2，将△EFG绕着点C旋转一个角度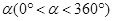
. 在旋转过程中，点E与点C重合，F的对应点为F′，G的对应点为G′. 设直线F′G′与射线DC、射线AC分别相交于M、N两点.试问：是否存在点M、N，使得△CMN是以∠MCN为底角的等腰三角形？若存在，请求出线段CM的长度；若不存在，请说明理由.
（本题满分8分．为方便答题，可在答卷上画出你认为必要的图形）
如图，在正方形ABCD中，点E，F分别在边BC，CD上，AE，BF交于点O，∠AOF＝90°．
求证：BE＝CF．
为了解中考体育科目训练情况，某县从全县九年级学生中随机抽取了部分学生进行了一次中考体育科目测试（把测试结果分为四个等级：A级：优秀；B级：良好；C级：及格；D级：不及格），并将测试结果绘成了如下两幅不完整的统计图．请根据统计图中的信息解答下列问题：
（1）本次抽样测试的学生人数是；
（2）图1中∠α的度数是，并把图2条形统计图补充完整；
（3）该县九年级有学生3500名，如果全部参加这次中考体育科目测试，请估计不及格的人数为．
（4）测试老师想从4位同学（分别记为E、F、G、H，其中E为小明）中随机选择两位同学了解平时训练情况，请用列表或画树形图的方法求出选中小明的概率．
本题满分7分．
如图，要利用一面墙（墙长为25米）建羊圈，用100米的围栏围成总面积为400平方米的三个大小相同的矩形羊圈，求羊圈的边长AB，BC各为多少米？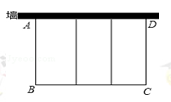
（本题满分7分．为方便答题，可在答卷上画出你认为必要的图形）
如图，矩形ABCD的对角线相交于点O，DE∥AC，CE∥BD．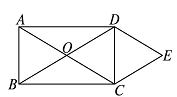
求证：四边形OCED是菱形．
解方程：x（x－2）＋x－2＝0．