（年江苏苏州10分）如图，二次函数（其中a，m是常数，且a>0，m>0）的图象与x轴分别交于点A，B（点A位于点B的左侧），与y轴交于点C(0，－3)，点D在二次函数的图象上，CD∥AB，连接AD．过点A作射线AE交二次函数的图象于点E，AB平分∠DAE．

（1）用含m的代数式表示a；
（2）)求证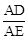：为定值；
（3）设该二次函数图象的顶点为F．探索：在x轴的负半轴上是否存在点G，连接CF，以线段GF、AD、AE的长度为三边长的三角形是直角三角形？如果存在，只要找出一个满足要求的点G即可，并用含m的代数式表示该点的横坐标；如果不存在，请说明理由．

科目 数学   题型 解答题   难度 中等