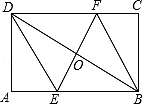
(2014年贵州贵阳12分)如图,将一副直角三角形拼放在一起得到四边形ABCD,其中∠BAC=45°,∠ACD=30°,点E为CD边上的中点,连接AE,将△ADE沿AE所在直线翻折得到△AD′E,D′E交AC于F点.若AB=6 cm.
cm.

(1)AE的长为 cm;
(2)试在线段AC上确定一点P,使得DP+EP的值最小,并求出这个最小值;
(3)求点D′到BC的距离.
如图,在△ ABC中,∠ ABC=90°,以 AB的中点 O为圆心, OA为半径的圆交 AC于点 D, E是 BC的中点,连结 DE、 OE.
(1)判断 DE与⊙ O的位置关系,并说明理由.
(2)求证: BC 2=2 CD• OE.

为了了解某市八年级学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况,某记者开展了一次抽样调査,根据调查结果绘制了如下尚不完整的统计图
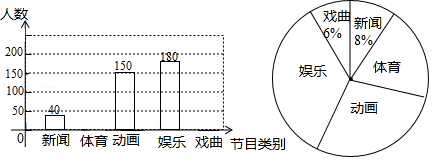
根据以上信息解答下列问题
(1)这次接受调查的八年级学生总人数为多少?
(2)扇形统计图中"动画"对应扇形的圆心角度数为多少?
(3)请补全条形统计图.
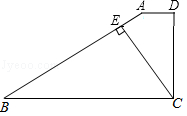
如图,在梯形 ABCD中, AD∥ BC,∠ ADC=90°,∠ B=30°, CE⊥ AB,垂足为点 E.若 AD=1, AB=4 ,求△ BCE外接圆的面积.
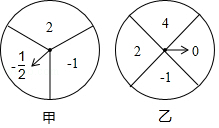
如图为甲、乙两个可以自由转动的均匀的转盘,甲转盘被分成3个面积相等的扇形,乙转盘被分成4个面积相等的扇形,每一个扇形都标有相应的数字,同时转动两个转盘,当转盘停止后,设甲转盘中指针所指区域内的数字为 m,乙转盘中指针所指区域内的数字为 n(若指针指在边界线上时,重转一次,直到指针指向一个区域为止)
(1)请你用画树状图或列表的方法求出 m和 n的乘积为偶数的概率;
(2)直接写出点( m, n)落在函数 y=﹣4 x图象上的概率.
如图,矩形 ABCD中,过对角线 BD中点 O的直线分别交 AB, CD边于点 E、 F.
(1)求证:四边形 BEDF是平行四边形;
(2)只需添加一个条件,即 ,可使四边形 BEDF为菱形.