(年福建龙岩13分)如图,在△ABC中,AB=AC=10,BC=12,D,E分别是边BC,AB的中点,P是BC边上的动点(不与B,C重合).设BP=x.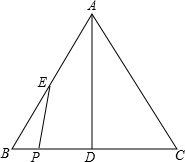
(1)当x=6时,求PE的长;
(2)当△BPE是等腰三角形时,求x的值;
(3)当AD平分EP时,试判断以EP为直径的圆与直线AC的位置关系,并说明理由.
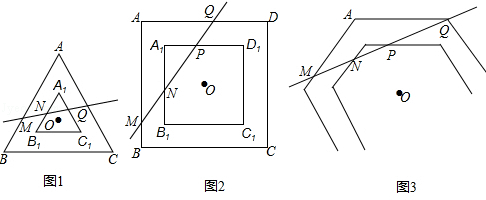
(1)如图1,两个等边三角形ABC和A1B1C1的中心(点O)相同,且满足AB∥A1B1,BC∥B1C1,AC∥A1C1,可知AB与 A1B1,BC与B1C1,AC与A1C1之间的距离相等,直线MQ分别交三角形相邻两边于点M、N、P、Q,与AB所成夹角为∠α,
①当∠α=30°时,求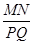 的值;
的值;
②当30°<∠α<90°,请用含∠α的式子表示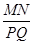 ;
;
(2)如图2,两个正方形ABCD和A1B1C1D1的中心(点O)相同,且满足AB∥A1B1,BC∥B1C1,CD∥C1D1,AD∥A1D1,可知AB与A1B1,BC与B1C1,CD与C1D1,AD与A1D1之间的距离相等,直线MQ分别交正方形相邻两边于点M、N、P、Q,与AB所成夹角为∠α,
①当∠α=30°时,求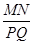 的值;
的值;
②当0°<∠α<90°,请用含∠α的式子表示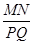 ;
;
(3)根据(1)、(2)的研究,如果正n边形(n>4)的位置关系也满足同样的条件(如图3),正n边形相邻两边被直线MQ截得的两条线段为MN,PQ,请用含m,∠α(0°<∠α<90°)的式子表示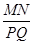 .
.
已知二次函数h=x2﹣(2m﹣1)x+m2﹣m(m是常数,且m≠0)
(1)证明:不论m取何值时,该二次函数图象总与x轴有两个交点;
(2)若A(n﹣3,n2+2)、B(﹣n+1,n2+2)是该二次函数图象上的两个不同点,求二次函数解析式和m的值;
(3)设二次函数h=x2﹣(2m﹣1)x+m2﹣m与x轴两个交点的横坐标分别为x1,x2(其中x1>x2),若y是关于m的函数,且y=2﹣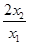 ,请结合函数的图象回答:当y<m时,求m的取值范围.
,请结合函数的图象回答:当y<m时,求m的取值范围.
如图,在△ABC中,AB=AC=4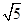 ,sinC=
,sinC=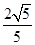 ,
,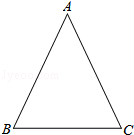
(1)求BC的长;
(2)作以AC为直径的⊙O,使⊙O交线段AB于点D,交线段BC于点E,并求点D到BC的距离(要求:尺规作图,保留作图痕迹,不写画法)
已知:如图,在△ABC中,D是BC边上的一点,E是AD的中点,过点A作BC的平行线交与BE的延长线于点F,且AF=DC,连接CF.
(1)求证:D是BC的中点;
(2)当AB与AC有何数量关系时,四边形ADCF为矩形,请说明理由.
如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,点A,B,C的坐标分别为(0,﹣1),(1,﹣1),(5,﹣1)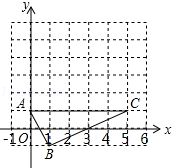
(1)判断△ABC的形状;
(2)将△ABC绕点C顺时针旋转90°得到△A1B1C,请在网格中画出△A1B1C,并直接写出点A1和B1的坐标;
(3)将△ABC绕线段AC所在直线旋转一周,求所得几何体的表面积.