（年山西省11分）课程学习：正方形折纸中的数学．
动手操作：如图1，四边形ABCD是一张正方形纸片，先将正方形ABCD对折，使BC与AD重合，折痕为EF，把这个正方形展平，然后沿直线CG折叠，使B点落在EF上，对应点为B′．
数学思考：（1）求∠CB′F的度数；
（2）如图2，在图1的基础上，连接AB′，试判断∠B′AE与∠GCB′的大小关系，并说明理由；
解决问题：
（3）如图3，按以下步骤进行操作：
第一步：先将正方形ABCD对折，使BC与AD重合，折痕为EF，把这个正方形展平，然后继续对折，使AB与DC重合，折痕为MN，再把这个正方形展平，设EF和MN相交于点O；
第二步：沿直线CG折叠，使B点落在EF上，对应点为B′，再沿直线AH折叠，使D点落在EF上，对应点为D′；
第三步：设CG、AH分别与MN相交于点P、Q，连接B′P、PD′、D′Q、QB′，试判断四边形B′PD′Q的形状，并证明你的结论．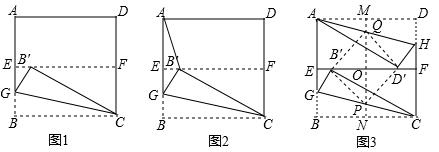
（本小题满分12分）在平面直角坐标系
中，已知抛物线
经过（2，1）和（6，-5）两点．
（1）求抛物线的解析式；
（2）设此抛物线与
轴交于A、B两点（点A在点B的左侧），与
轴交于C点，点P是在直线
右侧的这一抛物线上一点，过点P作PM
轴，垂足为M．若以A、P、M为顶点的三角形与△OCB相似，求点P的坐标．
（本小题满分10分）已知等腰△ABC和⊙M，且AB=AC．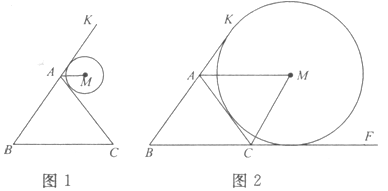
（1）如图l，若⊙M与BA的延长线AK及边AC均相切，求证：AM∥BC；
（2）如图2，若∠B=60°，⊙M与BA的延长线AK、BC的延长线CE及边AC均相切，求证：四边形ABCM是平行四边形．
（本小题满分l0分）有一批图形计算器，原售价为每台800元，在甲、乙两家公司销售．甲公司用如下方法促销：买一台单价为780元，买两台每台都按760元出售．依此类推，即每多买一台则所买各台单价均再减20元，但最低不能低于每台440元；乙公司则一律按原售价的75％促销．某单位需购买一批图形计算器：
（1）若此单位需购买8台图形计算器，则去哪家公司购买花费较少?
（2）若此单位恰好花费7500元，在同一家公司购买了一定数量的图形计算器，请问是在哪家公司购买的，数量是多少?
（本小题满分8分）有3张不透明的卡片，除正面写有不同的数字外，其它均相同．将这三张卡片背面朝上洗匀后，第一次从中随机抽取一张，并把这张卡片标有的数字记作一次函数表达式中的
，第二次从余下的两张卡片中再随机抽取一张，上面标有的数字记作一次函数表达式中的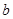
．
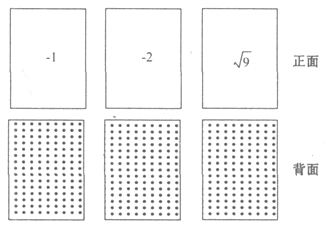
（1）写出为负数的概率；
（2）求一次函数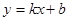
的图象经过二、三、四象限的概率。（用树状图或列表法求解）
（本小题满分7分）先化简、再求值：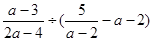
，其中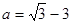
．