(2014年福建漳州12分)阅读材料:如图1,在△AOB中,∠O=90°,OA=OB,点P在AB边上,PE⊥OA于点E,PF⊥OB于点F,则PE+PF=OA.(此结论不必证明,可直接应用)
(1)【理解与应用】
如图2,正方形ABCD的边长为2,对角线AC,BD相交于点O,点P在AB边上,PE⊥OA于点E,PF⊥OB于点F,则PE+PF的值为 .
(2)【类比与推理】
如图3,矩形ABCD的对角线AC, BD相交于点O,AB=4,AD=3,点P在AB边上,PE∥OB交AC于点E,PF∥OA交BD于点F,求PE+PF的值;
(3)【拓展与延伸】
如图4,⊙O的半径为4,A,B,C, D是⊙O上的四点,过点C,D的切线CH,DG相交于点M,点P在弦AB上,PE∥BC交AC于点E,PF∥AD于点F,当∠ADG=∠BCH=30°时,PE+PF是否为定值?若是,请求出这个定值;若不是,请说明理由.

某气球内充满一定质量的气体,当温度不变时,气球内气体的气压p(kPa)是气体体积V(m3)的反比例函数,其图象如图所示.
(1)写出这一函数的表达式.
(2)当气体体积为1 m3时,气压是多少?
(3)当气球内的气压大于140 kPa时,气球将爆炸,为了安全考虑,气体的体积应不大于多少?
如图,E、F是□ABCD对角线 上的两点,且
上的两点,且 .
.
求证:(1) ;
;
(2) .
.
已知,如图,AB、DE是直立在地面上的两根立柱.AB=5m, 某一时刻AB在阳光下的投影BC=3m.
(1)请你在图中画出此时DE在阳光下的投影.
(2)在测量AB的投影时,同时测量出DE在阳光下的投影长为6m,请你计算DE的长.
“一方有难,八方支援”.今年11月2日,某县出现洪涝灾害,牵动着全县人民的心,县人民医院准备从甲、乙、丙三位医生和A、B两名护士中选取一位医生和一名护士支援防汛救灾工作.
(1)若随机选一位医生和一名护士,用树状图(或列表法)表示所有可能出现的结果.
(2)求恰好选中医生甲和护士A的概率.
某厂规定,该厂家属区的每户居民如果一个月的用电量不超过A度,那么这个月该户只要交10元用电费,如果超过A度,则这个月仍要交10元用电费外,超过部分还要按每度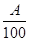 元交费.
元交费.
(1)该厂某户居民2月份用电90度,超过了规定的度,则超过部分应交费________元.(用含A的式子表示);
(2)下表是这户居民3月,4月的用电情况和交费情况.
| 月份 |
用电量(度) |
交电费总数(元) |
| 3月 |
80 |
25 |
| 4月 |
45 |
10 |
根据上表的数据,求该厂规定的A是多少?