（2014年江西抚州10分）【试题背景】
已知：l∥m∥n∥k，平行线l与m、m与n、n与k之间的距离分别为d1、d2、d3，且d1=d3=1，d2=2．我们把四个顶点分别在l、m、n、k这四条平行线上的四边形称为“格线四边形”．
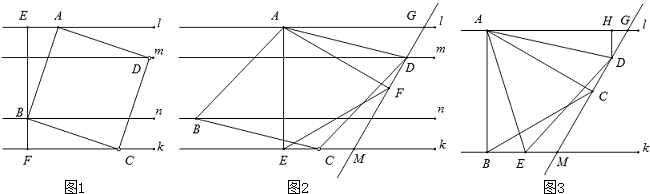
【探究1】
（1）如图1，正方形ABCD为“格线四边形”，BE⊥l于点E，BE的反向延长线交直线k于点F，求正方形ABCD的边长．
【探究2】
（2）矩形ABCD为“格线四边形”，其长：宽=2：1，则矩形ABCD的宽为 ．（直接写出结果即可）
【探究3】
如图2，菱形ABCD为“格线四边形”且∠ADC=60°，△AEF是等边三角形，AE⊥k于点E，∠AFD=90°，直线DF分别交直线l、k于点G、点M．求证：EC=DF．
【拓展】
（4）如图3，l∥k，等边△ABC的顶点A、B分别落在直线l、k上，AB⊥k于点B，且AB=4，∠ACD=90°，直线CD分别交直线l、k于点G、点M、点D、点E分别是线段GM、BM上的动点，且始终保持AD=AE，DH⊥l于点H．
猜想：DH在什么范围内，BC∥DE？并说明此时BC∥DE的理由．
如图，已知抛物线y=ax2+bx+c（a≠0）经过A（﹣1，0），B（4，0），C（0，2）三点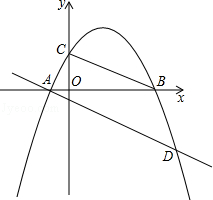
（1）求这条抛物线的解析式；
（2）E为抛物线上一动点，是否存在点E使以A、B、E为顶点的三角形与△COB相似？若存在，试求出点E的坐标；若不存在，请说明理由；
某企业设计了一款工艺品，每件的成本是50元，为了合理定价，投放市场进行试销．据市场调查，销售单价是100元时，每天的销售量是50件，而销售单价每降低1元，每天就可多售出5件，但要求销售单价不得低于成本．
求销售单价为多少元时，每天的销售利润最大？最大利润是多少？
如图，一次函数y=ax+b与反比例函数y=的图象交于A、B两点，点A坐标为（m，2），点B坐标为（﹣4，n），OA与x轴正半轴夹角的正切值为
，直线AB交y轴于点C，过C作y轴的垂线，交反比例函数图象于点D，连接OD、BD．
（1）求一次函数与反比例函数的解析式；
（2）求四边形OCBD的面积．
在一个口袋中有四个完全相同的小球，把它们分别标号为1,2, 3，4.小明和小强采取了不同的摸取方法，分别是：
小明：随机抽取一个小球记下标号，然后放回，再随机地摸取一个小球，记下标号；
小强：随机摸取一个小球记下标号，不放回，再随机地抽取一个小球，记下标号.
用画树状图（或列表法）分别表示小明和小强摸球的所有可能出现的结果；
分别求出小明和小强两次摸球的标号之和等于5的概率.
解不等式组：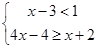
．